绘制更多的二维SDF形状

背景

在先前的教程中，我们已经了解了如何绘制简单的二维形状，如线段、圆形、正方形、长方形、圆角长方形等。但是，通过使用二维有符号距离场（SDF）运算，我们可以将这些基本形状组合在一起，创造出更为复杂的形状。这节内容我们就学习如果用这些简单的形状构造出复杂多变的形状。

圆

我们直接来看看绘制圆形的代码，具体原理不再多讲了啊，大家可以去看看前面的文档。

// Author: ice
// Title:

#ifdef GL_ES
precision mediump float;
#endif

uniform vec2 u_resolution;
uniform vec2 u_mouse;
uniform float u_time;


float sdfCircle(vec2 uv,float r){
 float d =length(uv)-r;
    return d;
}


void main() {
    vec2 uv = (gl_FragCoord.xy-.5*u_resolution.xy)/min(u_resolution.x,u_resolution.y);
    float dsdfCircle = sdfCircle(uv,0.05);
     dsdfCircle= step(0., dsdfCircle);

          vec3 col = vec3(dsdfCircle );
    gl_FragColor = vec4(col,1.0);
}

绘制正方形

绘制正方形我们前面也给大家详细介绍过其原理性内容，具体效果和代码如下所示：

// Author:
// Title:

#ifdef GL_ES
precision mediump float;
#endif

uniform vec2 u_resolution;
uniform vec2 u_mouse;
uniform float u_time;

float sdfBox(vec2 uv,float b){
    vec2 d = abs(uv)-b;
    return length(max(d,0.0)) + min(max(d.x,d.y),0.0) ;
}

void main() {
    vec2 uv = (gl_FragCoord.xy-.5*u_resolution.xy)/min(u_resolution.x,u_resolution.y);

    float dsdfBox = sdfBox(uv-vec2(0.1,0.1),.05);
  dsdfBox =  step(0., dsdfBox);
   
          vec3 col = vec3( dsdfBox );
    gl_FragColor = vec4(col,1.0);
}

正题

好了我们来看一下今天的正题，今天我们要实现图形求交集、并集等。

交集

求交集我们一般是用max函数，我们拿几何图形形象解释下。请看下图：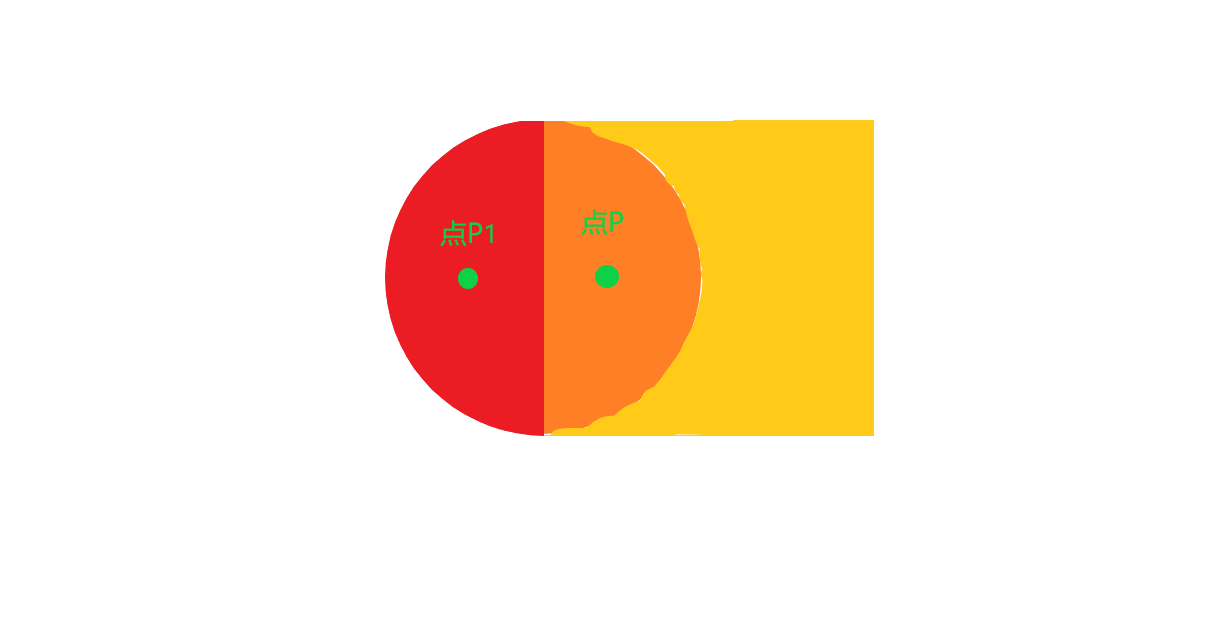

假设我们在max函数几何相交的部分有一点P,该P点如我们所看到的即在圆形里面，也在正方形里面。判别方法就是我们上面给大家复习的SDF知识，通过测算出是在几何图形边界的外面和里面，进而勾勒出几何的边界线。

通过运算我们可知P点与正方形和圆形的距离都是小于0，比如我们现在P点到正方形的距离为-0.1，到圆形的距离为-0.2，然后max函数得到值是d=-0.1，再代入到step(0,d)函数中，根据我们初级课程所讲述的，得到的结果必然就是小于0的，那么P点所呈现的结果就是黑色。

我们再假设一个点P1,如上图所示，P1点此刻的位置是在正方形外面，所以其到正方形的距离是大于0的，比如等于0.1,同时P1点此刻的位置是在圆形里面，所以其到圆形的距离是小于0的，比如等于0.1,那么max函数得到值是d=0.1，再代入到step(0,d)函数中，根据我们初级课程所讲述的，得到的结果必然就是大于0的，那么P点所呈现的结果就是白色。

依次类推，我们可以轻松的总结出以下规律：

冰哥说：原谅我没有找到分段函数的函数编写公式，但这一点不影响你们冰哥的讲解内容：当sdf圆和sdf正的距离都小于0时候，d最终结果也小于0，反之，如果sdf圆和sdf正有一个大于0，那么d最终结果就是大于0。这不恰恰是我们几何相交对应吗？

// Author:ice
// Title:

#ifdef GL_ES
precision mediump float;
#endif

uniform vec2 u_resolution;
uniform vec2 u_mouse;
uniform float u_time;

float sdfBox(vec2 uv,float b){
   vec2 d = abs(uv)-b;
    return length(max(d,0.0)) + min(max(d.x,d.y),0.0) ;
}
float sdfCircle(vec2 uv,float r){
    float d =length(uv)-r;
    return d;
}

void main() {
    vec2 uv = (gl_FragCoord.xy-.5*u_resolution.xy)/min(u_resolution.x,u_resolution.y);
    float dsdfCircle = sdfCircle(uv,0.05);
    float dsdfBox = sdfBox(uv-vec2(0.270,0.010),0.268);
  
    float d =  max(dsdfCircle,dsdfBox);
    d  = step(0., d );
    vec3 col = vec3( d );
    gl_FragColor = vec4(col,1.0);
}

并集

如果你理解上面的交集，那么接下来的并集就非常的easy了吧。合并我们用到的是min函数。这次我们继续拿点P做例子。

冰哥说：假设点P,不管是在正方形或者在圆形里面，或者即在圆形也在正方形里面，其sdf的值肯定有一个是小于0的，那再通过min函数取值，其结果肯定都是小于0的，初了上述三种情况外，还有一种情况就是即在圆形外也在正方形外，那么其sdf结果均为大于0的值，再通过min函数取值，其结果肯定都是大于0的。再代入到step(0,d)函数中，根据我们初级课程所讲述的，得到的结果必然是大于0的，那么P点所呈现的结果就是白色，反之小于0的，那么P点所呈现的结果就是黑色。

// Author:ice
// Title:

#ifdef GL_ES
precision mediump float;
#endif

uniform vec2 u_resolution;
uniform vec2 u_mouse;
uniform float u_time;

float sdfBox(vec2 uv,float b){
   vec2 d = abs(uv)-b;
    return length(max(d,0.0)) + min(max(d.x,d.y),0.0) ;
}
float sdfCircle(vec2 uv,float r){
    float d =length(uv)-r;
    return d;
}

void main() {
    vec2 uv = (gl_FragCoord.xy-.5*u_resolution.xy)/min(u_resolution.x,u_resolution.y);
    float dsdfCircle = sdfCircle(uv,0.05);
    float dsdfBox = sdfBox(uv-vec2(0.270,0.010),0.268);
  
    float d =  min(dsdfCircle,dsdfBox);
    d  = step(0., d );
    vec3 col = vec3( d );
    gl_FragColor = vec4(col,1.0);
}

相差

正方形-圆形

我们接下来看看两个几何图形如何做相减，接下来的这个例子我做了一个小圆和一个大的正方形，我想实现大正方形减去小圆圈，给大正方形掏一个小白洞。

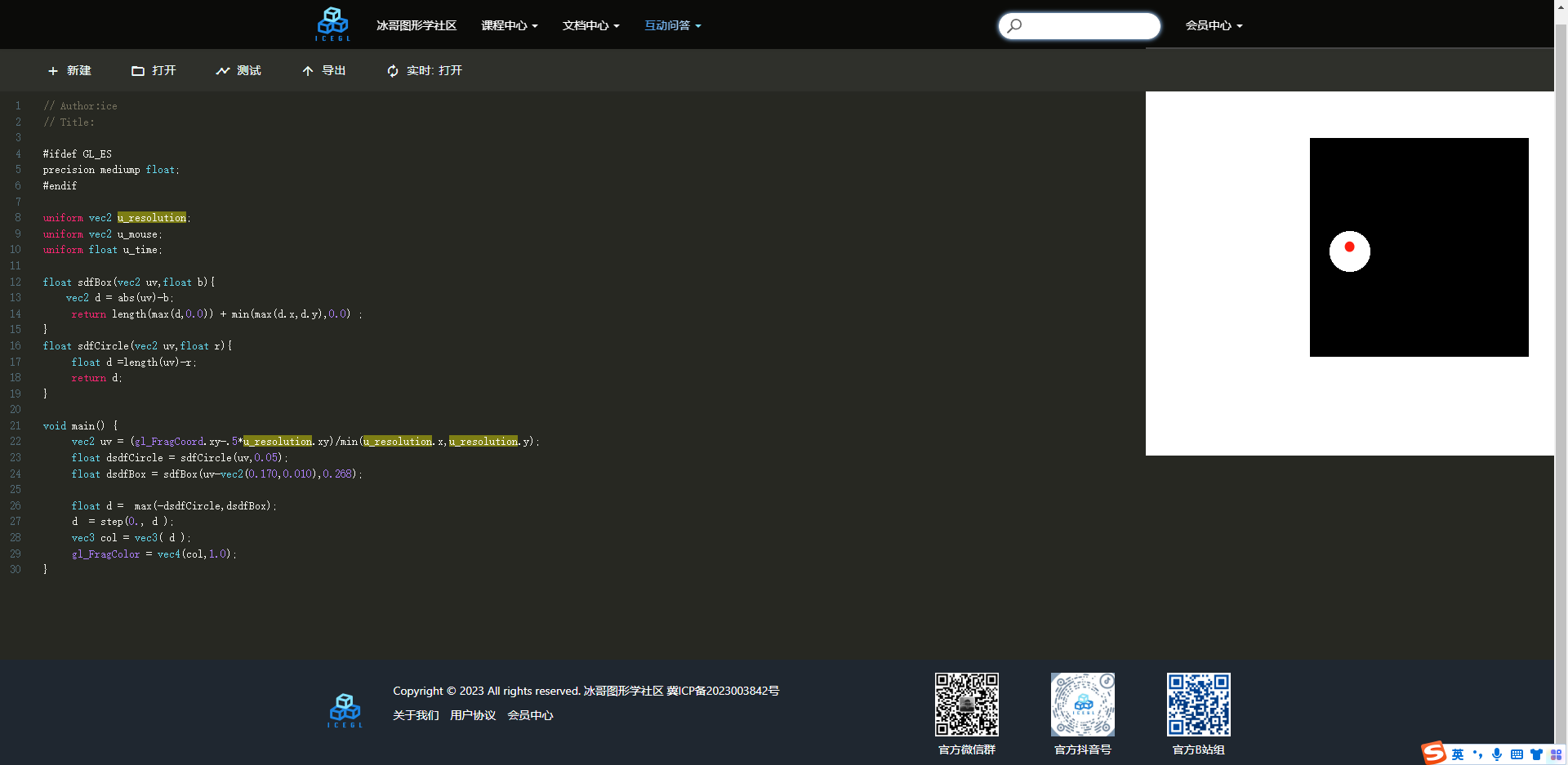
假设我们在小圆圈处有一红色点P，该点首先获得sdf圆的值是小于0的，sdf正方形的值也是小于0的，但是你需要留意的是我们在sdf圆的前面加了一个负号哦，说明在该位置他的sdf圆形的值变成大于0的了，sdf正方形的值还是小于0的哈，因为我们没有给他加任何操作。最后我们求max函数的时候，其值必然P点的值是大于0的，所以是白色，正方形的其他位置都是小于0的，必然都是黑色。那么正方形外面，因为sdf圆和sdf正方形都是大于0的，所以正方形外肯定都是白色的哈

// Author:ice
// Title:

#ifdef GL_ES
precision mediump float;
#endif

uniform vec2 u_resolution;
uniform vec2 u_mouse;
uniform float u_time;

float sdfBox(vec2 uv,float b){
   vec2 d = abs(uv)-b;
    return length(max(d,0.0)) + min(max(d.x,d.y),0.0) ;
}
float sdfCircle(vec2 uv,float r){
    float d =length(uv)-r;
    return d;
}

void main() {
    vec2 uv = (gl_FragCoord.xy-.5*u_resolution.xy)/min(u_resolution.x,u_resolution.y);
    float dsdfCircle =-sdfCircle(uv,0.05);
    float dsdfBox = sdfBox(uv-vec2(0.170,0.010),0.268);
  
    float d =  max(dsdfCircle,dsdfBox);
    d  = step(0., d );
    vec3 col = vec3( d );
    gl_FragColor = vec4(col,1.0);
}

圆形-正方形

反过来是一样的思路哈，如果你还不熟悉这个四维过程，我建议你还是以点P为例子，按照上述思考过程进行思考。实现代码如下，你可以参考！

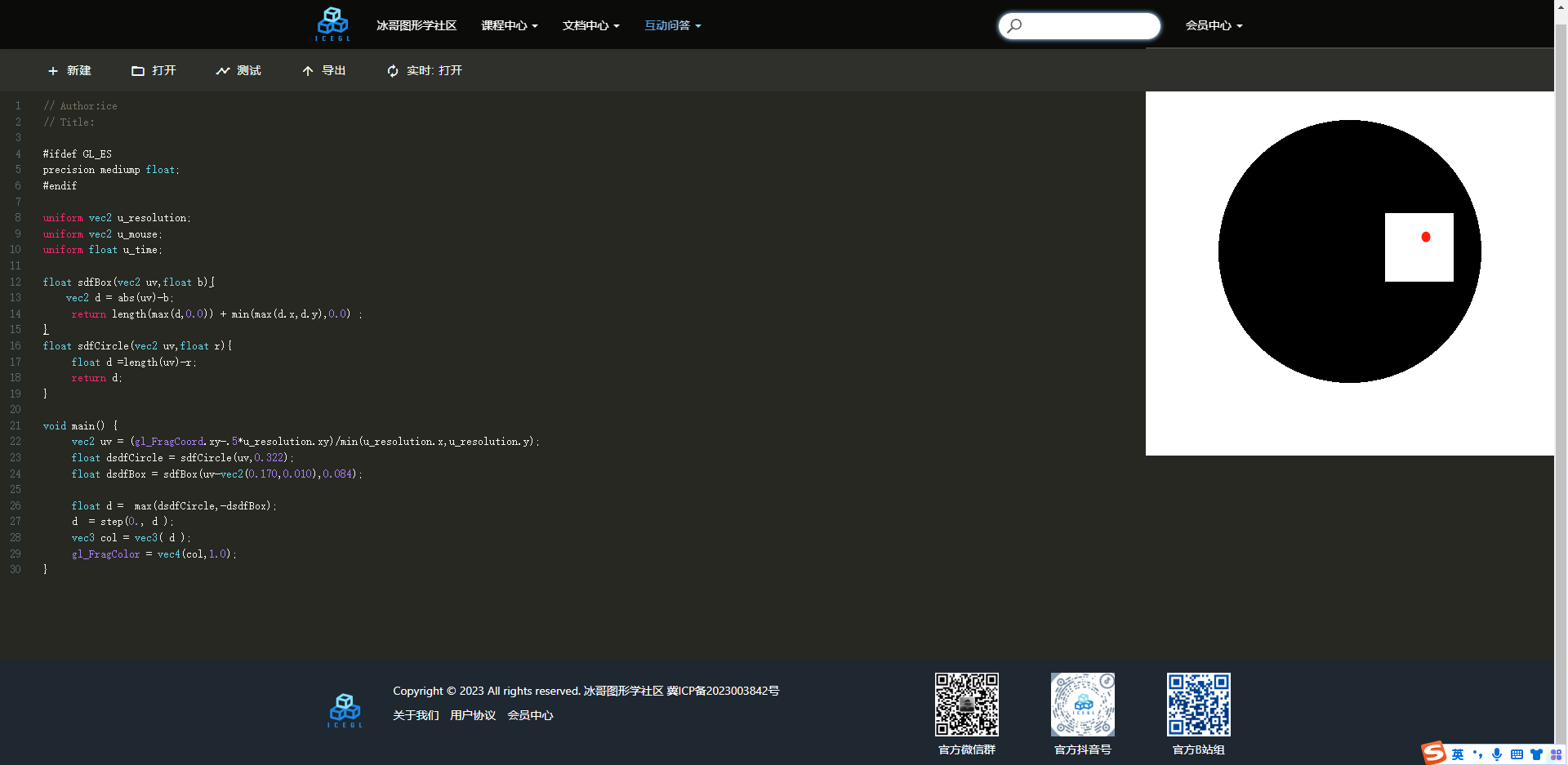
// Author:ice
// Title:

#ifdef GL_ES
precision mediump float;
#endif

uniform vec2 u_resolution;
uniform vec2 u_mouse;
uniform float u_time;

float sdfBox(vec2 uv,float b){
   vec2 d = abs(uv)-b;
    return length(max(d,0.0)) + min(max(d.x,d.y),0.0) ;
}
float sdfCircle(vec2 uv,float r){
    float d =length(uv)-r;
    return d;
}

void main() {
    vec2 uv = (gl_FragCoord.xy-.5*u_resolution.xy)/min(u_resolution.x,u_resolution.y);
    float dsdfCircle = sdfCircle(uv,0.322);
    float dsdfBox = sdfBox(uv-vec2(0.170,0.010),0.084);
  
    float d =  max(dsdfCircle,-dsdfBox);
    d  = step(0., d );
    vec3 col = vec3( d );
    gl_FragColor = vec4(col,1.0);
}

冰哥说：针对相减我想给你总结一个小规律，如果想要实现a-b,那么你只需要应用max函数，在被减数的sdf前面加一个负号就可以咯~

不相交

两个几何图形不相交部分我们可以基于上面的相交和并集得到，总的思路就是由并集部分减去相交部分剩下不就是不相交部分嘛。看一下下面图形。

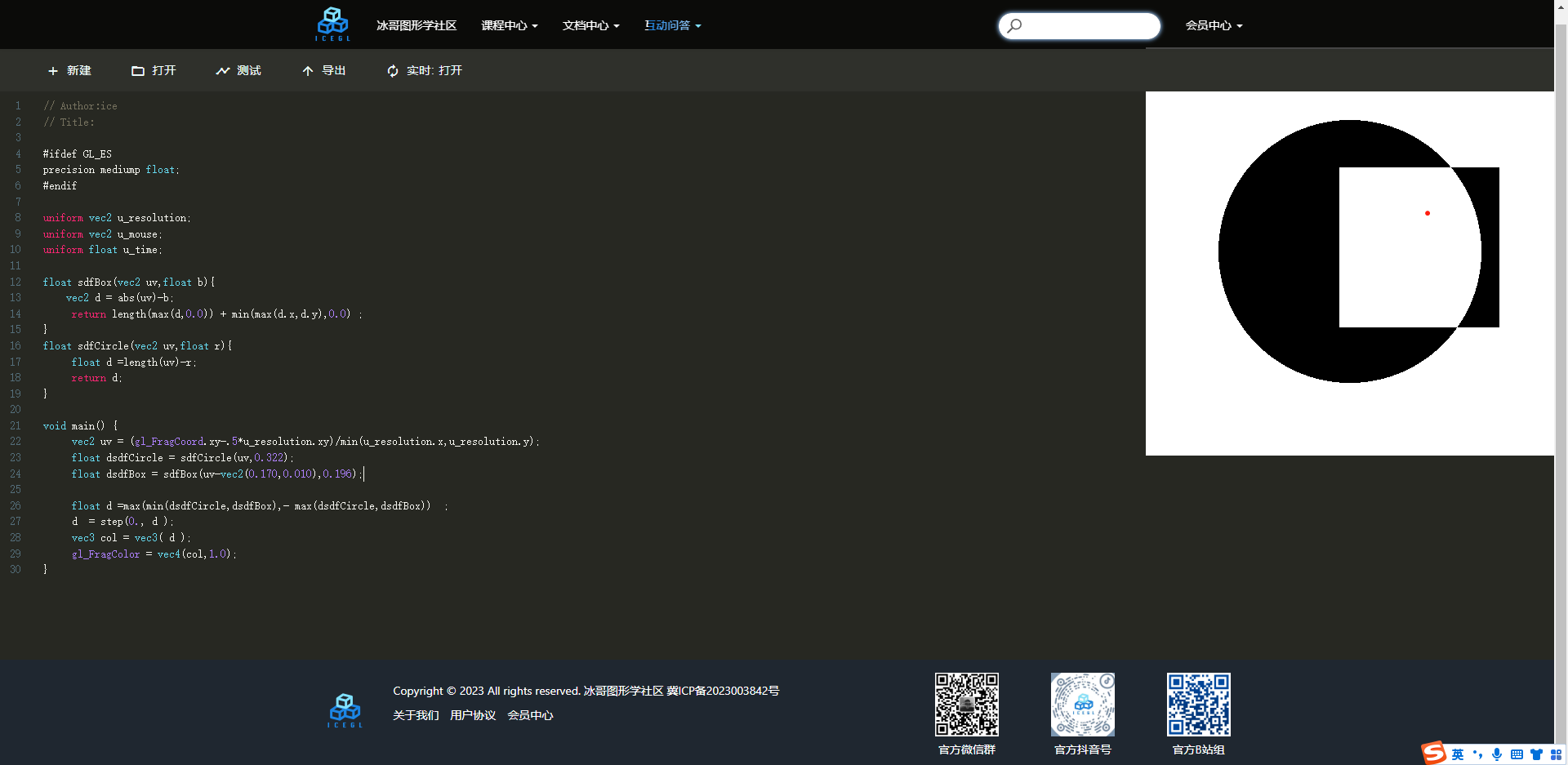
float d =max(min(dsdfCircle,dsdfBox),- max(dsdfCircle,dsdfBox)) ;这次我们换个思路，由代码结果反推道理。

最外层是max函数，其结果里面分别由两个参数组成： float d =max(并集,-交集) ;，由上面我们讲的如果求两个几何部分相减，你就可以在被减数前面加一个负号。由此我们可以从我们上述推论的规律总结，不想交的内容，快动手操作一番吧！

// Author:ice
// Title:

#ifdef GL_ES
precision mediump float;
#endif

uniform vec2 u_resolution;
uniform vec2 u_mouse;
uniform float u_time;

float sdfBox(vec2 uv,float b){
   vec2 d = abs(uv)-b;
    return length(max(d,0.0)) + min(max(d.x,d.y),0.0) ;
}
float sdfCircle(vec2 uv,float r){
    float d =length(uv)-r;
    return d;
}

void main() {
    vec2 uv = (gl_FragCoord.xy-.5*u_resolution.xy)/min(u_resolution.x,u_resolution.y);
    float dsdfCircle = sdfCircle(uv,0.322);
    float dsdfBox = sdfBox(uv-vec2(0.170,0.010),0.196);
  
    float d =max(min(dsdfCircle,dsdfBox),- max(dsdfCircle,dsdfBox)) ;
    d  = step(0., d );
    vec3 col = vec3( d );
    gl_FragColor = vec4(col,1.0);
}

冰哥说：我们本文所介绍的内容不仅在二维里面适用，同时完全适用于三维sdf,所以请大家务必好好理解！
我们这次内容就先讲解到这里，下节内容给大家带来更有意思的推论！