背景

SDF在图形学里算是很基础的理论知识，并且在其上，衍生了很多复杂的知识体系。SDF定义虽然简单，但是正因为其简单，所以给我们后期编程带来很大的遍历性，其规律和特性具有很好的复用性，封装成相应的函数，我们可以直接复制、粘贴，运行就可以产生想要的效果。

我在前面的课程里面，给大家推荐过shadertoy这个网站，这个神奇的网站背后的作者正是IQ大神，此外IQ还有自己专门的博客论坛，提供了大量的SDF模型，接下来我将利用最可能通俗易懂的话术，给大家讲解这一块内容，希望大家能够更加深刻理解其背后的含义。

点击到shadertoy网站里面的demo是可以查看其源码的，大家可以看完讲解后查看其源码，尝试修改其参数，当然我也会在我的B站课程里面讲解其原理，希望大家支持。

定义

官方定义：符号距离函数（sign distancefunction），简称SDF，又可以称为定向距离函数（oriented distance function），在空间中的一个有限区域上确定一个点到区域边界的距离并同时对距离的符号进行定义：点在区域边界内部为正，外部为负，位于边界上时为0。

冰哥理解：SDF实际的目的是为了区别出图形体，内部和外部的数值变化。听着还是很抽象是吧，那再具体一些，我们前面都知道shader实际上是对每一个像素进行控制，在实际中大家一定听过世界中太平洋和大西洋海水交会，在交会处颜色有差异性变化，造成这方面原因是海水密度不同。shader也是一样的问题，通过交界线两侧数值不一样，可以明显的将边界线进行标绘，这样其实也就顺理成章达成了我们的目标---绘制图形。

2D SDF模型

圆形

圆形是最好理解的，因为其结构简单，线条一气呵成，距离表示不用分情况讨论。

float sdCircle( vec2 p, float r )
{
return length(p) - r;
}

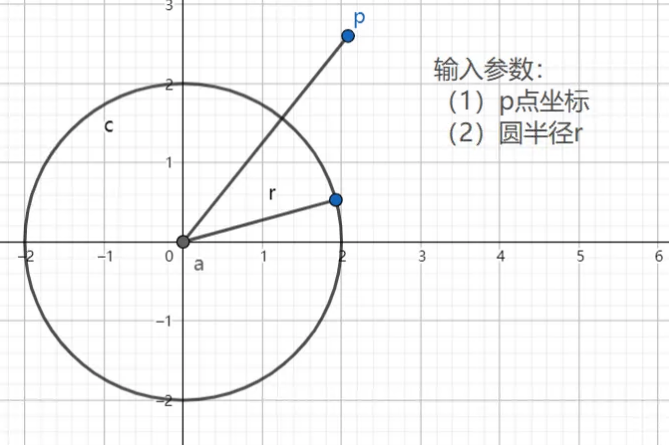
以上式子分别传入的是任意一点p和半径r，那么数学问题来了，求点p到圆上的最短距离d？实际上我们用函数图形很容易明白这一点原理：

$$ d=\sqrt{p.x^{2} + p.y^{2}} - r $$

将其精简一点，利用shader中内置函数可以变形为：

$$ d=length(p)-r $$

注：我们通过这个简单例子可以洞察到如果某个点在圆内，此时的d是小于0的；如果某个点在圆外，此时d是大于0的；如果某个点在圆内，此时d是等于0的。

OK，相信你已经有了一定的认识，让我们加大点难度。

线段

float sdSegment( in vec2 p, in vec2 a, in vec2 b )
{
    vec2 pa = p-a, ba = b-a;
    float k = clamp( dot(pa,ba)/dot(ba,ba), 0.0, 1.0 );
    return length( pa - ba*k );
}

以上式子，我们分别传入了任意点p，起点a，终点b。我们现在的目的还是求到线段的最短距离d。 有的人肯定会问，为什么画一根线，要绕这么一大圈，为什么要求到线段的最短距离呢？这个问题实际上是一种解决问题的思路，本质原因还是在我最开始文章中举得例子，求出任意点与当前图形的里外关系，即可表示出界限，虽然线段是一个一维图形，但是他里面仍然是由密密麻麻的像素点所拼接，所以我们同样可以采取这个思路去表示这条线段，其实规范化术语也就是SDF，让我们不断去深入理解SDF，come on 老baby！

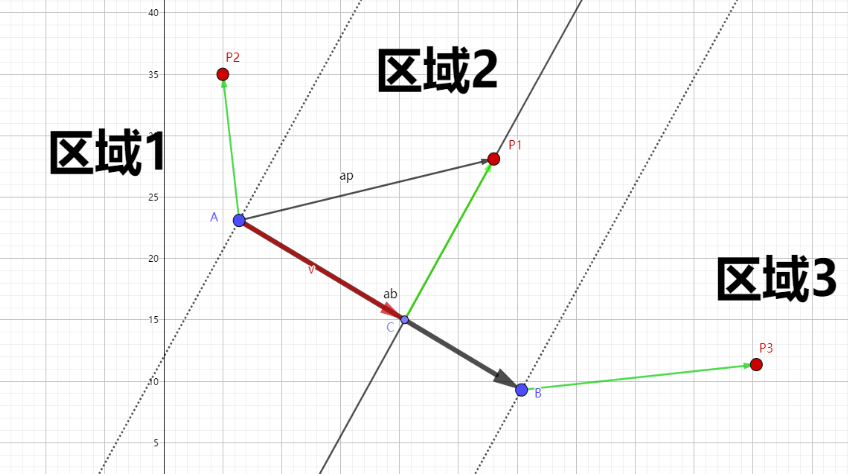
首先我们观察上面的图形解释，我们将任意一条起点为a，重点为b的线段均可以分割成三部分，区域1，区域2和区域3。

区域2

在三个区域中我们率先去看区域2中的P1点，如果我们现在求P1点到线段的最短距离d等于多少？

$$ d=|AP1-AC| = |AP-kAB| $$

首先来解释下AC（是向量AP1在向量AB方向的投影向量）我们来看根据向量减法，我们可以得到P1点到向量AB的最短距离向量（垂线），最后再求距离就可以得到最终的距离d。之后我们又做了一步，就是将此公式改成了更为通用的公式就是|AP-kAB|。因为刚才讲到AC本身就是AB向量的一部分，所以表示为k倍的AB也没有毛病吧。

区域1

第二个来看区域1，区域1中任意点P2到线段的最短距离是多少呢？这好像是个小学知识，但往往也最容易让我们忽略。

$$ d=|AP2| = |AP-kAB|(k=0) $$

这里面稍微耍了一个滑头，就是我们又将公式抽象成了通用公式，也就是引入了k值，此时k值正好等于0的时候，恰好是我们最短距离。

区域3

第三个来看区域3，区域3任意点P3到线段的最短距离是多少呢？实际上他和区域1是类似的，但这里也用到我们向量减法。

$$ d=|BP3| = |AP3-kAB| = |AP-kAB| （k=1） $$

我们这里也将式子归纳为与k有关的等式。就这样我们完成很关键的一步，就是我们将多种不同情况的结果都归纳总结为一个等式去表示，这在数学和物理中里面非常常见。

$$ d=|AP-kAB|(0<=k<=1) $$

注：这里我们要做一个阶段性总结：

a、b、p三个点都是我们函数中传入的点，所以在上式中我们对于最短距离d的表示所有的未知数目前只剩下k值了对吧，因为k值是任意变化的所以我们同样要用a、b、p三个点表示出来。

k值

那么k等于多少呢，实际上我们在几何意义上已经给大家做了解释，就是k是AC在AB向量上面的一个参数比例关系。接下里看等式，公式看着复杂实际上很简答，只是为了表达详细些，有理可循。请耐心看。

$$ k = \frac{\left|AP\right|\left|AB\right|cos\theta }{\left|AB\right|\left|AB\right|cos\left(0\right)} = \frac{\left|AP\right|cos\theta }{\left|AB\right|cos\left(0\right)} = \frac{\left|AP\right|cos\theta }{\left|AB\right|*1} = \frac{\left|AC\right|}{\left|AB\right|}\:\: $$

最后我们将上述公式改写成shader函数自带的公式

$$ k=dot(ap,ab)/dot(ab,ab) $$

希望大家记住这个公式，非常经典且简洁，这个公式整理成一句话就是：求一条线在另一条线上的投影比例。

clamp()

这个函数我们在中级课程中讲解过，他是返回规定区间内的值。因为我们在上述几何推理中或者了k的取值范围是[0,1]，所以clamp将k的值严格限定在这个范围 内，方便后面去合理运算。

注：最后为了加深理解，回过头来思考下，线段的SDF的本质还是将SDF上下左右以及线上所有点与边界的位置关系都表示出来，我们继续带着这个理论基点研究下面的2D SDF。

综上所示，以上是对线段的所有解释，希望对你有所帮助

矩形

float sdBox( in vec2 p, in vec2 b )
{
    vec2 d = abs(p)-b;
    return length(max(d,0.0)) + min(max(d.x,d.y),0.0);
}

先来看第一象限的情况，矩形本身以及红色虚线把第一象限分成①②③④四部分，最短距离d:

区域1

$$ d=|AP1| =\sqrt{\left(p.x - a.x\right)^{2} + \left(p.y - a.y\right)^{2}} $$

区域1中的任意点P到A点的最短距离，表达式如上所示，我相信大家应该没啥问题哈。

区域2

$$ d=p.y-a.y $$

区域2中任意点P到A点的最短距离，是P点与A点纵坐标相减，公式如上所示。那多考虑一下，此时p.x-a.x是正数还是负数，从图上我们可以一眼看出答案，就是小于0的。

区域3

$$ d=p.x-a.x $$

区域3中任意点P到A点的最短距离，是P点与A点横坐标相减，公式如上所示。那多考虑一下，此时p.y-a.y是正数还是负数，从图上我们可以一眼看出答案，就是小于0的。

归纳公式

依据我们之前线段的规律，就是尽量将多种情况，尽可能归纳成一个公式。

$$ d = \sqrt{\max \left(\left(p.x−a.x,0\right)2^{} + \max \left(\left(p.y−a.y,0\right)2^{}\right.\right.} $$

接下里解释下这个阶段性公式，max函数我们在中级的时候给大家讲过，这个函数返回的是两个值中最大的一个，举个具体的例子p.x-a.x如果此时是大于0的，则返回p.x-a.x，如果p.y-a.y此时是大于0的，则返回p.y-a.y。大家发现了吗，这种情况恰巧是我们的区域1的情况。再举个例子p.x-a.x如果此时大于0，则返回p.x-a.x，如果此时p.y-a.y此时是小于0的，则返回0，那么d=p.x-a.x，这不恰巧就是区域3吗？区域2的情况是同样的道理。

此公式如果再精简一些，就是下面的这个公式：

$$ d=|max(p-a,0)| $$

区域4

此时大家一定会问区域4怎么处理呢，我们将区域4里面的数据带入到上述式子中，d=0。我们在之前也讲过，我们总结式子的最终目的就是将图形区域两侧通过正负关系进行区别开，现在区域4明明是在正方形里面，但是d的值是0，所以是有问题的。我们需要将区域4进行单独的表示。先看公式吧，逐公式去解释：

$$ \min \left(\max \left(p.x - a.x,p.y - a.y\right),0\right) $$

max函数里面，刚才介绍了返回是最大的一个结果。假设此时区域4存在点P，点P与点A，横纵坐标相减都是负数，因为我们的目的是求到矩形边界的最短距离，max函数返回的结果就是任意点P到矩形边界的最短距离的结果（此时的距离是有负号的哈，距离的长度越长，值越大），此外再对比min函数，这个函数返回的是结果中最小的值，因为此时距离有负号，值一定是比0小的，所以min返回还是这个带负号的距离值。那这样我们的区域4内的点都已经被表示出来了。

再次归纳

区域1，区域2，区域3，【d=|max(p-a,0)|】，区域4【 min(max(q.x, q.y), 0.0)】，再将这4个区域总结归纳为统一函数如何处理呢，先看式子：

$$ d=|max(p-a,0)|+\min \left(\max \left(p.x - a.x,p.y - a.y\right),0\right) $$

我对两个式子做了相加，第一个式子带入区域1，区域2和区域3中的点都能满足要求，但带入区域4是等于0，加号右边的式子和恰恰相反，带入区域4是能满足要求，但是带入其他的正好是返回0，那将两个式子相加正好返回其结果哈。

注：因为IQ作者在自己博客中写到，为了方便推论和理解，将整个图形是以原点为中心，我们目前的长方形满足关于x,y对称要求的，所以我们只需要将任意点P取绝对值，就可以实现关于x,y这种对称关系，我们目前求出来的区域1经过x，y对称，就可以得到完整的长发形哈！

参考文献

IQ博客：https://iquilezles.org/articles/distgradfunctions2d/

shaderToy实例：https://www.shadertoy.com/playlist/MXdSRf

借用工具

公式编辑器：https://www.imathtool.com/edit/

函数关系推演器：https://www.geogebra.org/classic#cas

实例

巧用线段的SDF去绘制sin函数