背景

欧拉角是由于数学家莱昂哈德·保罗·欧拉提出来的，几年前第一次听到欧拉角的时候，索性看了看这位伟大数学家的历史，发现莱昂哈德·保罗·欧拉真是一位传奇人物，欧拉晚年饱受眼疾的病痛，但是欧拉的学术生产力似乎并未受到病痛影响，大概归因于他的心算能力和超群的记忆力。据说他平均每周完成一篇数学论文，可想而知其多么牛！

附赠一张MJ自动生成的欧拉头像...

1783年9月18日，晚餐后，欧拉一边喝着茶，一边和小孙女玩耍，突然之间，烟斗烟斗)从他手中掉了下来。他说了一声：“我的烟斗”，并弯腰去捡，结果再也没有站起来，他抱着头说了一句：“我死了”。“欧拉停止了计算和生命”。

哪怕伟大的人流逝了，但他的思想留存了下来。接下里我们来完全理解下欧拉角的原理与应用。

定义

依靠我的个人的理解以及我阅读了大量的文献，将欧拉角定义分解成了几个要点，方便大家理解：

• 任意一个旋转都可以用相互垂直的三个轴来表示，这三个轴我们一般采用的是笛卡尔坐标系（其实任意轴都可以，只不过笛卡尔坐标系最有意义）
• 旋转后，原来互相垂直的轴可能不再垂直，当前步骤只能影响下一个旋转步骤，不能影响之前的旋转步骤
• 这里默认右手坐标系，逆时针为正，任意三个轴可以作为旋转轴。
• 物体坐标系中我们称三个基本轴向叫（heading、pitch、bank）；惯性坐标系我们成为（yaw、pitch、roll）；这两组叫法分别对应（y、x、z）

  注：如果大家不清楚惯性坐标系和物体坐标系，移步这里坐标系简介

下面这张图是分别针对物体坐标系和惯性坐标系的理解：

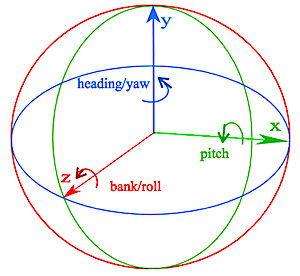
欧拉角其实是比较好理解的，这也是他最优秀的点。

优缺点

优点

1. 直观易懂。它比矩阵和四元数简单得多，这可能是因为欧拉角中的数都是角度，符合人们思考方位的方式。如果我们选择了与所要处理的情况最符合的约定，那么就能直接描述出最重要的角度，例如，用 heading-pitch-bank 系统就能直接地描述出偏差角度。
2. 最简洁的表达方式。欧拉角用三个数来表达方位。在 3D 中，表达方位不能少于三个数。
3. 内存占用少。只用三个数，你想想吧。
4. 任意三个数都是合法的。取任意三个数，它们都能构成合法的欧拉角，而且可以把它看成一个对方位的描述。从另一方面说，没有“不合法”的欧拉角。当然，数值可能不对，但至少它们是合法的。可矩阵和四元数就不一定是这样了。

缺点

1. 欧拉角存在万向锁问题。当第二个旋转角接近90度时，第一个旋转角和第三个旋转角将被锁定在同一平面内，导致旋转变得异常困难。万向锁等会我们重点谈。
2. 不唯一性。同一个物体的旋转可以使用多组不同的欧拉角来表示。这导致了解析度问题，并且对于某些任务，精度可能会受到影响。比如：120度和480度是一样的位置，他们中间多加了360度。
3. 顺序问题。欧拉角需要按照特定的顺序进行旋转，例如“先绕X轴旋转，再绕Y轴旋转，最后绕Z轴旋转”。如果顺序不正确，则结果可能会出错。一般在引擎里面都可以设定旋转顺序。这块非常重要，其实顺序的设定是万向锁造成的一个原因。

1. 对计算机不友好。欧拉角需要进行角度转换和三角函数计算，这些操作对于计算机来说是非常昂贵的。此外，由于欧拉角存在一些数学问题，因此在编写程序时需要仔细考虑这些问题。
2. 两个欧拉角间求插值比较难。

万向锁

万向锁有的地方也叫万向死锁。我的定义理解是：如果一个物体首先围绕其X轴进行旋转，然后围绕其Y轴进行旋转，最后围绕其Z轴进行旋转，那么在Y轴旋转为90度时会发生万向锁问题。这是因为在这个时候，X和Z轴会对齐，使得旋转轴的自由度降低到两个，从而导致旋转结果出现异常。

我们来用threejs动画形式来表示下万向锁。

实际在例子中，我初始化值的时候另y轴旋转到了90度，然后此时我转动z和x，发现二者转动方向是一致的，这就应征了一些书上提到的欧拉角消失了一个维度。下面是我定义欧拉角的数值：

const a = new THREE.Euler( 0, Math.PI/2, 0, 'XYZ' );

在这里我们稍微拓展下threejs的知识，下面是关于threejs 欧拉角构造函数的理解。

Euler( x : Float, y : Float, z : Float, order : String )
x - (optional) 用弧度表示x轴旋转量。 默认值是 0。
y - (optional) 用弧度表示y轴旋转量。 默认值是 0。
z - (optional) 用弧度表示z轴旋转量。 默认值是 0。
order - (optional) 表示旋转顺序的字符串，默认为'XYZ'（必须是大写）。

其中关键点在于order属性，他定义了threejs中旋转的顺序。这一点极为重要，你要时刻记住对欧拉角的变换是有序的 ，变换的顺序是预先确定的顺序而非实际输入的顺序。

我们先提一嘴结论，稍后通过实例测试一下：当前步骤只能影响下一个旋转步骤，不能影响之前的旋转步骤，通俗来讲上述x轴的变换影响y和z，y可以影响z，但是y不能影响x，z更不能影响x和y。我建议你看一下这个视频万向锁几何解释，这个视频的特点在于他通过一个现实中的机械物件，模拟出了万向锁的现象，但整个视频就是围绕我上述讲的结论进行论述的。

看完上述视频，我想你大概能理解在几何上的万向锁概念，根据上述推测，以threejs为例const a = new THREE.Euler( 0, Math.PI/2, 0, 'XYZ' );中的XYZ代表的是旋转顺序。如果是XYZ，那么Y是90度，那么X和Z会丢失一个维度；同样道理，如果此时是YXZ，如果X是90度，那么Y和Z也会丢失一个维度；如果此时是YXZ，X是90度，那么Y和Z也会丢失一个维度。当然还有其他多种组合方式（A33种）。这其实和我们在一些书中总结万向锁概念不谋而合,“这种角度为±90°的第二次旋转使得第一次和第三次旋转的旋转轴相同的现象,称作万向锁”。接下里我们用threejs印证下我们的猜想，我以YXZ为例，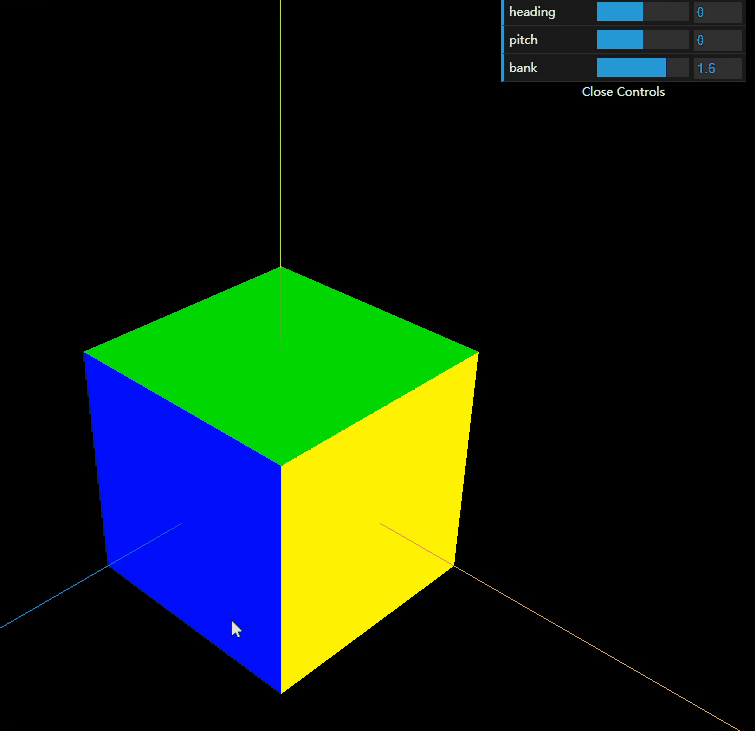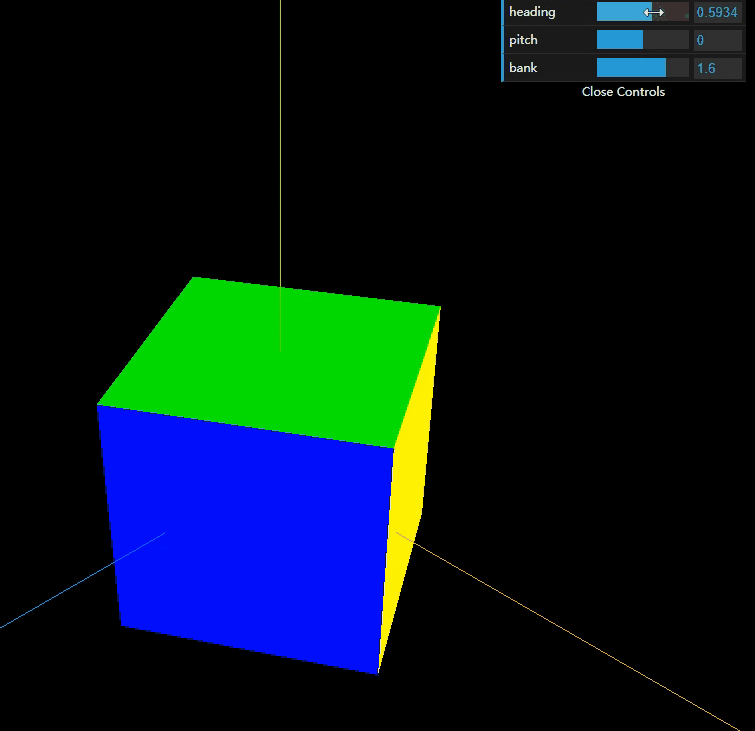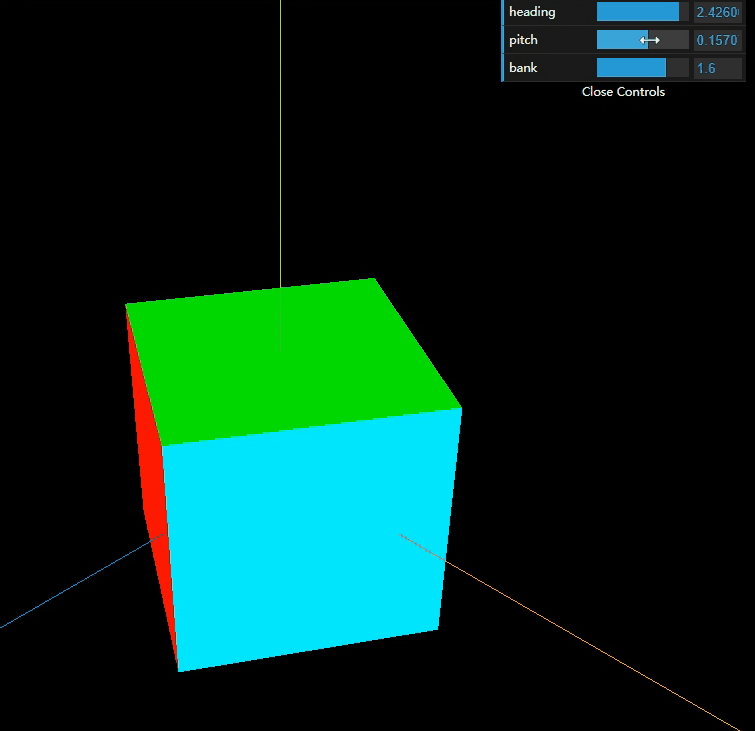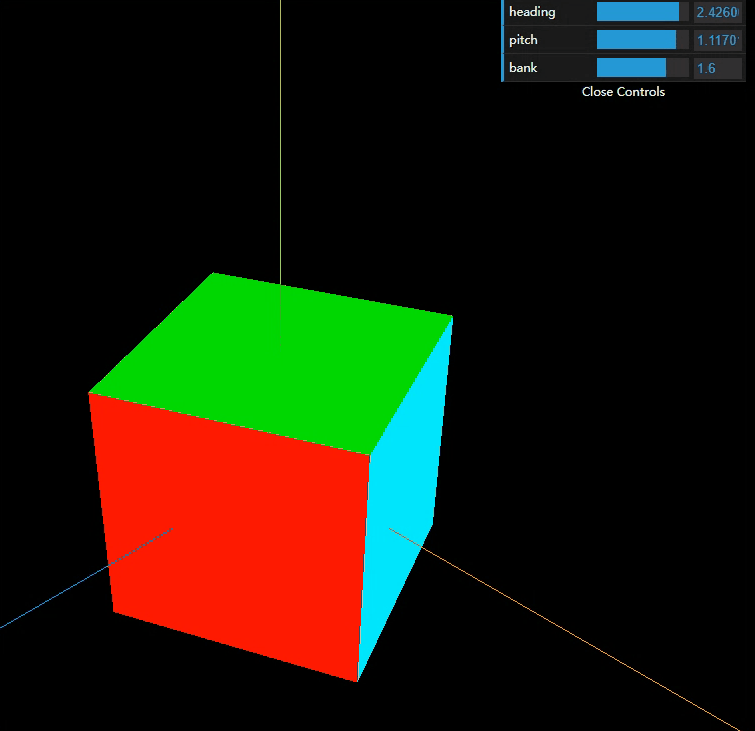

实例证明，规律确实如此。如果在旋转Y的时候，Y转动，XZ也会随着转动，但是因为X和Z始终垂直，所以不会出现万向锁的现象，但如果X转动的时候，Y是不会转动的，但是Z是会随着转动的，恰恰当X等于90度的，Y和Z重合了，所以就会出现万向锁。这样说大家应该是可以理解万向锁的现象了吧。

但是有个要命的问题就出现了，为什么欧拉角会遵循“当前步骤只能影响下一个旋转步骤，不能影响之前的旋转步骤“？他似乎像咒怨一样，阴魂不散，又像是欧拉角自诞生后就一直存在的问题，确实如此....

解答这个问题，还是得需要从欧拉角的定义入手，再强调一点就是欧拉角只是一种状态的描述，并不是描述的过程，这就说明为什么我们直接给的一个欧拉角就不会存在万向锁，但是如果一连续的变化某个值，就会出现万向锁。所谓的状态就是比如你正在吃饭、你吃完饭了，这就是一直状态，是你当前的欧拉角度的描述，但是至于你怎么吃饭，吃的什么这是过程。给定一个欧拉角比如（100,90,120），它只是定义了这种状态，并不是从1度慢慢变换到当前度数的。

代数理解

最初我们讲解欧拉角的时候就提到，空间中任意一个旋转都可以拆解成沿着物体自身三个正交坐标轴的旋转，用公式表示如下：

$$ E(bank，heading，pitch)=R_z(bank)R_y(heading)R_x(pitch) $$

我们来回忆一下关于旋转矩阵的定义：

$$ \begin{gathered} R_{x}(\theta) =\begin{bmatrix}1&0&0\\ 0&\cos(\theta)&-\sin(\theta)\\ 0&\sin(\theta)&\cos(\theta)\end{bmatrix} \\ R_y(\theta) =\begin{bmatrix}\cos(\theta)&0&\sin(\theta)\\ 0&1&0\\ -\sin(\theta)&0&\cos(\theta)\end{bmatrix} \\ R_z(\theta) =\begin{bmatrix}\cos(\theta)&-\sin(\theta)&0\\[6pt]\sin(\theta)&\cos(\theta)&0\\[6pt]0&0&1\end{bmatrix} \end{gathered} $$

我们前面提到过，欧拉角的旋转顺义很重要，矩阵也不例外，不满足交换律。如果我把把旋转矩阵的公式带入到R_z(bank)R_y(heading)R_x(pitch),得到的结果是什么呢？

$$ E(\alpha,\frac{\pi}{2},\beta)=R_z(\beta)R_y(\frac{\pi}{2})R_x(\alpha) $$

已知

$$ R_\x(\alpha)=\begin{bmatrix}1&0&0\\ 0&\cos\alpha&-\sin\alpha\\ 0&\sin\alpha&\cos\alpha\end{bmatrix},\quad R_\y(\frac\pi2)=\begin{bmatrix}0&0&1\\ 0&1&0\\ -1&0&0\end{bmatrix},\quad R_\z(\beta)=\begin{bmatrix}\cos\beta&-\sin\beta&0\\ \sin\beta&\cos\beta&0\\ 0&0&1\end{bmatrix} $$

带入到上述公式，其中满足矩阵乘法口诀，注意认真一些化简的时候，不过还需要注意三角函数化简的公式，我罗列到下面（和差公式）：

$$ \begin{gathered} \sin(a\pm b) =\sin a\cos b\pm\cos a\sin b \\ \cos(a \pm b) =\cos a\cos b\mp\sin a\sin b \end{gathered} $$

最后化简完成后，如下所示：

$$ \begin{aligned} E(\alpha,{\frac{\pi}{2}},\beta)& =R_{z}(\beta)R_{y}(\frac{\pi}{2})R_{x}(\alpha) \\ &=\begin{bmatrix}0&\cos(\beta)\cdot\sin(\alpha)-\cos(\alpha)\cdot\sin(\beta)&\sin(\alpha)\cdot\sin(\beta)+\cos(\alpha)\cdot\cos(\beta)\\ 0&\sin(\alpha)\cdot\sin(\beta)+\cos(\alpha)\cdot\cos(\beta)&\cos(\alpha)\cdot\sin(\beta)-\cos(\beta)\cdot\sin(\alpha)\\ -1&0&0\end{bmatrix} \\ &=\begin{bmatrix}0&\sin(\alpha-\beta)&\cos(\alpha-\beta)\\ 0&\cos(\alpha-\beta)&-\sin(\alpha-\beta)\\ -1&0&0\end{bmatrix} \end{aligned} $$

最后的结果其实可以再次化简：

$$ R_{y}(\frac{\pi}{2})R_{x}(\alpha-\beta) $$

通过最后的结论我想结果也就不言而喻了，变量中只有y和x，z消失了！，所以这就印证了少了一个维度,此时就会发生万向锁。

还有一个点没有讲就是欧拉与四元数和矩阵之间的互转问题...后续我们聊完四元数再来补充，或者再在连载中讲解。