图形学中Phong高光反射公式数学推演

发布于 2023-06-08 15:51:04

概述

最近有小伙伴问我，在网上看了很多关于Phong模型中高光公式的推广，感觉越看越糊涂，并且很多都是错的，或者结果是对的但是中间推导基本是囫囵吞枣，搞得晕头转向。今天我们专门针对这个小知识点来做讲解。主要是数学知识的运用哈！

首先帮助大家甄别一下下面的博文，结果是对的但是中间讲解很敷衍，有的甚至是错误的，希望大家少踩坑。

错误1.png

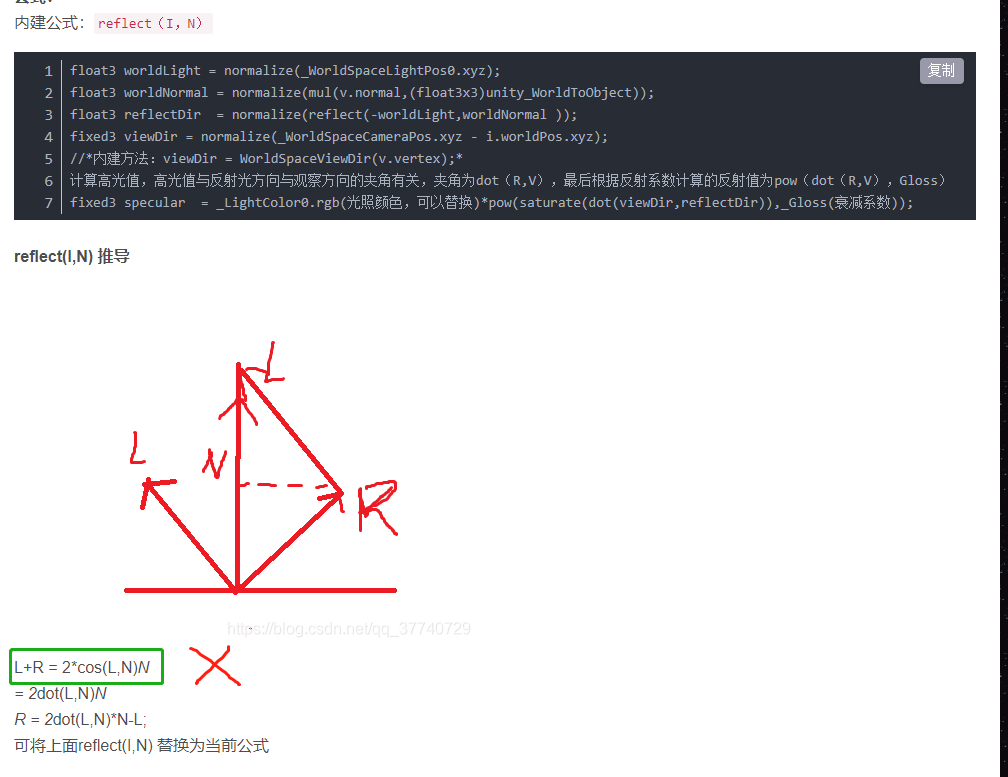
(17条消息) UnityShader 笔记_淡定看世界的博客-CSDN博客

还有这篇文章，我发现很多地方引用了此篇文章，尤其csdn上，但是讲解的非常粗略，容易让人一头雾水。

(17条消息) Unity Shader-Phong光照模型与Specular_puppet_master的博客-CSDN博客

以上并没有贬低的意思，希望大家能够甄别出坑来，尽量输出准确的答案。我们接下来看一下下面的内容。

Phong模型我们不再过多的解释，今天我们只讲解其中一小部分，“镜面反射”。下面是“镜面反射”的原理图。

高光.png

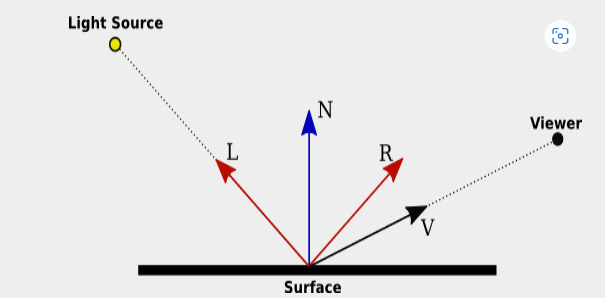
在现实生活中，金属和抛光表面等材料具有镜面反射，根据相机角度或观察者面对物体的位置，它们看起来会更亮。因此，我们的目的是求的相机视角和反射光线的夹角，想象一下，如果我们在太阳光下看一个镜子，镜子里反射回来很亮很亮的一个光斑。这就是其中一个高光的现实例子。

高光现实.png

基础知识

基础知识我们不过多去赘述，大家回忆一下向量，向量加法，向量的点乘以及向量的模等概念，如果不明白的可以翻翻以前的文章或者自行百度一下。

向量投影

向量投影.png

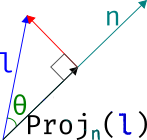
向量投影我们需要复习下，上图表达的是向量l在向量n上的投影向量，那么用数学公式表示如下所示：

$$ P(l)=\hat{n}∗f $$

$$ 其中f是一个标量，是l在n上的投影长度，向量\hat{n}是向量n的单位向量。 $$

现在我们来求f的值：

$$ f = |l|cos(θ) $$

那么得：

$$ P(l)=\hat{n}∗ |l|cos(θ) $$

再之后我们根据点乘公式可以得到：

$$ l·n = |l||n|cos(θ) $$

$$ cos(θ) =(l·n)/|l||n| $$

进而我们得到：

$$ P(l) = \hat{n} * |l|((l·n)/|l||n|) = \hat{n} * (l·n)/|n| $$

再变形：

$$ P(l) = n/|n| * (l·n)/|n|=n * (l·n)/|n|²=n * (l·n)/(n·n) $$

反射向量

下图是反射的向量模型，我们最终目的是要求R向量。我们已知的参数值是向量L和向量N。

计算过程高光.png

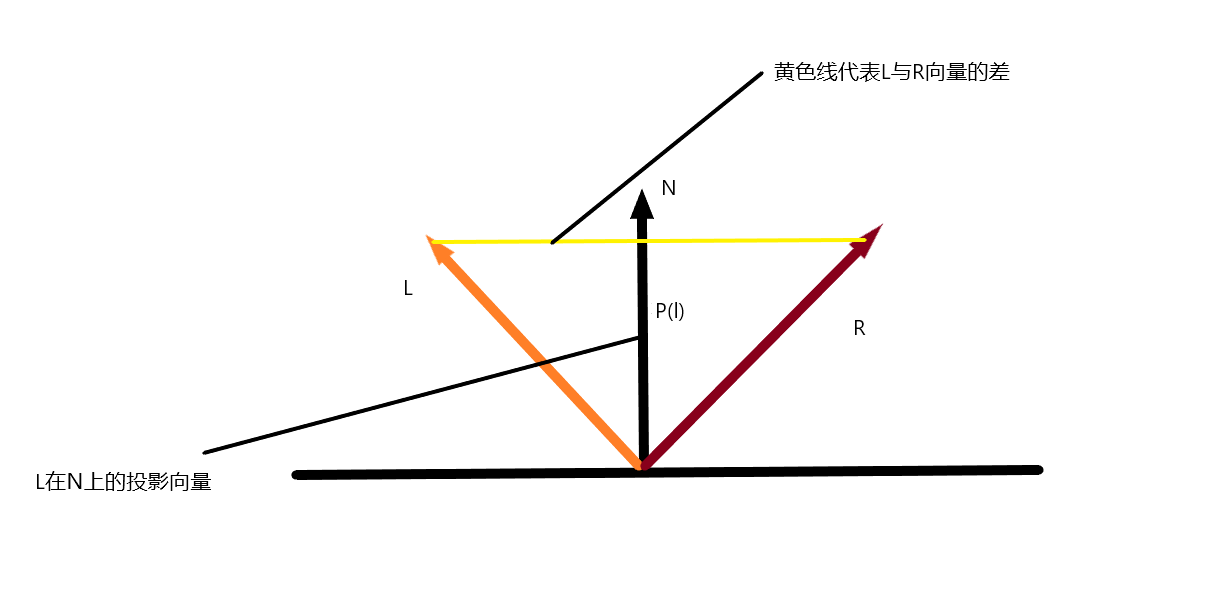
我们由上面向量L在向量N的投影等于：

$$ P(l) = n * (l·n)/(n·n) $$

那么我们可以求的图上黄色细线的向量为：

$$ Q= 2(L-P(l)) $$

那么向量R等于

$$ L-R = Q $$

所以：

$$ R = L-Q = L-2(L-P(l))= 2P(l)-L =2*n * (l·n)/(n·n)-l $$

$$ 最后，如果n首先是一个单位向量（长度为 1 的向量），然后|n|=1，还有就是向量\hat{n}=n。 $$

所以最终公式变形为：

$$ R =2*n * (l·n)-l $$

应用

上述推导出来的公式实际上在glsl已经给我们封装成一个函数名字叫做：reflect,我再glsl中级课程中讲到了此函数的应用。

求出反射光线来我们需要和相机的向量求的二者之间的夹角，就像上面我们提到，如果相机方向和反射方向正好在一条直线上，那么此时肯定是最了“刺眼”的,所以我需要又要用到点乘然后判断二者之间的夹角。代码一版如下所示：

 float dotRV = clamp(dot(-reflect(lightDirection, normal), -eyedirection), 0., 1.);

一般如果你觉得高亮对比度还不够高，我们可以用pow函数去加大对比度。

 vec3 specular =  pow(dotRV, 50.) ;

下面给大家列举了一个demo。gl-matrix.js大家自行在官网下载最新的就可以https://glmatrix.net/

<!--
 * @Descripttion: 
 * @version: 
 * @Author: Jsonco
 * @Date: 2023-06-29 
 * @LastEditors: sueRimn
 * @LastEditTime: 2022-06-19 14:57:14
-->
<!DOCTYPE html>
<html lang="en">

<head>
    <meta charset="UTF-8">
    <meta http-equiv="X-UA-Compatible" content="IE=edge">
    <meta name="viewport" content="width=device-width, initial-scale=1.0">
    <title>Document</title>
    <script src="gl-matrix.js"></script>
    <script>
        let vertexstring = `
        attribute vec4 a_position;
        uniform mat4 u_formMatrix;
        attribute vec4 a_Normal;
        varying vec4 v_Normal;
        varying vec4 v_position;
        void main(void){
        gl_Position = u_formMatrix * a_position;
        v_position = gl_Position;
        v_Normal= a_Normal;
        }
        `;
        let fragmentstring = `
        precision mediump float;
   
        varying vec4 v_Normal;
        varying vec4 v_position;
        uniform vec3 u_PointLightPosition;
        uniform vec3 u_DiffuseLight;
        uniform vec3 u_AmbientLight;

        uniform vec3 u_eyedirection;
        void main(void){
        vec3 normal = normalize(v_Normal.xyz);
        vec3 lightDirection = normalize(u_PointLightPosition - vec3(v_position.xyz));
        float nDotL = max(dot(lightDirection, normal), 0.0);
        vec3 diffuse = u_DiffuseLight * vec3(1.0,0,1.0)* nDotL;
        vec3 ambient = u_AmbientLight * vec3(1.0,0,1.0);
   
        vec3 sp=reflect(lightDirection,v_Normal.xyz);
        vec3  halfLE   = normalize(lightDirection + u_eyedirection);
        vec3 eyedirection = normalize(u_eyedirection);
        // vec3 specular = pow(clamp(dot(v_Normal.xyz, halfLE), 0.0, 1.0), 50.0)*vec3(1.);
         vec3 specular=pow(clamp(-dot(sp,eyedirection),0.,1.),10.)*vec3(1.);

          gl_FragColor =vec4(diffuse + ambient+specular, 1);
        }
        `;

        var webgl;
        var angle = 45;
        var webglDiv
        function init() {
            initWebgl();
            initShader();
            initBuffer();
            draw();
        }

        function initWebgl() {
            webglDiv = document.getElementById('myCanvas');
            webgl = webglDiv.getContext("webgl");
            webgl.viewport(0, 0, webglDiv.clientWidth, webglDiv.clientHeight);

        }
        function initShader() {

            let vsshader = webgl.createShader(webgl.VERTEX_SHADER);
            let fsshader = webgl.createShader(webgl.FRAGMENT_SHADER);

            webgl.shaderSource(vsshader, vertexstring);
            webgl.shaderSource(fsshader, fragmentstring);

            webgl.compileShader(vsshader);
            webgl.compileShader(fsshader);
            if (!webgl.getShaderParameter(vsshader, webgl.COMPILE_STATUS)) {
                var err = webgl.getShaderInfoLog(vsshader);
                alert(err);
                return;
            }
            if (!webgl.getShaderParameter(fsshader, webgl.COMPILE_STATUS)) {
                var err = webgl.getShaderInfoLog(fsshader);
                alert(err);
                return;
            }
            let program = webgl.createProgram();
            webgl.attachShader(program, vsshader);
            webgl.attachShader(program, fsshader)
            webgl.linkProgram(program);
            webgl.useProgram(program);
            webgl.program = program

        }
        var positions = [];
        var indices = [];
        var normals = [];
        function initBuffer() {

            var SPHERE_DIV = 16;

            var i, ai, si, ci;
            var j, aj, sj, cj;
            var p1, p2;
         

            // Generate coordinates
            for (j = 0; j <= SPHERE_DIV; j++) {
                aj = j * Math.PI / SPHERE_DIV;
                sj = Math.sin(aj);
                cj = Math.cos(aj);
                for (i = 0; i <= SPHERE_DIV; i++) {
                    ai = i * 2 * Math.PI / SPHERE_DIV;
                    si = Math.sin(ai);
                    ci = Math.cos(ai);

                    positions.push(si * sj);  // X
                    positions.push(cj);       // Y
                    positions.push(ci * sj);  // Z

                   
                    normals.push(si * sj,cj,ci * sj);
                }
            }
            console.log("positions",positions);
            // Generate indices
            for (j = 0; j < SPHERE_DIV; j++) {
                for (i = 0; i < SPHERE_DIV; i++) {
                    p1 = j * (SPHERE_DIV + 1) + i;
                    p2 = p1 + (SPHERE_DIV + 1);

                    indices.push(p1);
                    indices.push(p2);
                    indices.push(p1 + 1);

                    indices.push(p1 + 1);
                    indices.push(p2);
                    indices.push(p2 + 1);
                }
            }

            let pointPosition = new Float32Array(positions);
            let aPsotion = webgl.getAttribLocation(webgl.program, "a_position");
            let triangleBuffer = webgl.createBuffer();
            webgl.bindBuffer(webgl.ARRAY_BUFFER, triangleBuffer);
            webgl.bufferData(webgl.ARRAY_BUFFER, pointPosition, webgl.STATIC_DRAW);
            webgl.enableVertexAttribArray(aPsotion);
            webgl.vertexAttribPointer(aPsotion, 3, webgl.FLOAT, false, 0, 0);

            let aNormal = webgl.getAttribLocation(webgl.program, "a_Normal");
            let normalsBuffer = webgl.createBuffer();
            let normalsArr = new Float32Array(normals);
            webgl.bindBuffer(webgl.ARRAY_BUFFER, normalsBuffer);
            webgl.bufferData(webgl.ARRAY_BUFFER, normalsArr, webgl.STATIC_DRAW);
            webgl.enableVertexAttribArray(aNormal);
            webgl.vertexAttribPointer(aNormal, 3, webgl.FLOAT, false, 0, 0);

            let u_DiffuseLight = webgl.getUniformLocation(webgl.program, 'u_DiffuseLight');
            webgl.uniform3f(u_DiffuseLight, 1.0, 1.0, 1.0);
            let u_LightDirection = webgl.getUniformLocation(webgl.program, 'u_PointLightPosition');
            webgl.uniform3fv(u_LightDirection, [3.0, 3.0, 4.0]);
            let u_AmbientLight = webgl.getUniformLocation(webgl.program, 'u_AmbientLight');
            webgl.uniform3f(u_AmbientLight, 0.2, 0., 0.2);

            let u_Eyedirection = webgl.getUniformLocation(webgl.program, 'u_eyedirection');
            webgl.uniform3fv(u_Eyedirection, [0, 0, 7]);



            let indexBuffer = webgl.createBuffer();
            let indices1 = new Uint8Array(indices);
            webgl.bindBuffer(webgl.ELEMENT_ARRAY_BUFFER, indexBuffer);
            webgl.bufferData(webgl.ELEMENT_ARRAY_BUFFER, indices1, webgl.STATIC_DRAW);





            //矩阵变换
            let ProjMatrix = glMatrix.mat4.create();
            glMatrix.mat4.identity(ProjMatrix);
            //角度小，看到的物体大，角度大，看到的物体小。
            glMatrix.mat4.perspective(ProjMatrix, angle * Math.PI / 180, webglDiv.clientWidth / webglDiv.clientHeight, 1, 1000)    //修改可视域范围

            let uniformMatrix1 = webgl.getUniformLocation(webgl.program, "u_formMatrix");

            let ModelMatrix = glMatrix.mat4.create();
            glMatrix.mat4.identity(ModelMatrix);
            glMatrix.mat4.translate(ModelMatrix, ModelMatrix, [0, 0, 0]);

            let ViewMatrix = glMatrix.mat4.create();
            glMatrix.mat4.identity(ViewMatrix);
            glMatrix.mat4.lookAt(ViewMatrix, [3, 3, 7], [0, 0, 0], [0, 1, 0]);

            let mvMatrix = glMatrix.mat4.create();
            glMatrix.mat4.identity(mvMatrix);
            glMatrix.mat4.multiply(mvMatrix, ViewMatrix, ModelMatrix);

            let mvpMatrix = glMatrix.mat4.create();
            glMatrix.mat4.identity(mvpMatrix);
            glMatrix.mat4.multiply(mvpMatrix, ProjMatrix, mvMatrix);
            webgl.uniformMatrix4fv(uniformMatrix1, false, mvpMatrix)

        }
        function createData() {

        }
        function draw() {
            webgl.clearColor(0, 0, 0, 1);
            webgl.clear(webgl.COLOR_BUFFER_BIT | webgl.DEPTH_BUFFER_BIT);
            webgl.enable(webgl.DEPTH_TEST);

            webgl.drawElements(webgl.TRIANGLES, indices.length, webgl.UNSIGNED_BYTE, 0);


        }


    </script>
</head>

<body onload="init()">
    <canvas id='myCanvas' width="1024" height='768'></canvas>
    <div id="text"></div>
</body>

</html>

1 条评论

Jsonco 2023-06-09

奔驰的蜗牛

注：需要注意的是reflect函数对应的值$$R =l-2*n * (l·n)$$,和我们上面推广出来的结果是相反数，其原因也很简单，这与我们入射光线的方向有直接关系，我们现在假设光线方向是指向光源的，推出来的式子就是$$R =2*n * (l·n)-l$$。这点就需要我们根据实际情况去选择使用。

请登录后再发布评论，点击登录

关于作者

Jsonco

奔驰的蜗牛

文章

回答

被采纳

关注TA

发私信

shader绘制二维爱心

图形学中Phong高光反射公式数学推演

概述

基础知识

向量投影

反射向量

应用

关于作者

Jsonco

相关文章

热门问题

热门标签

推荐达人

图形学中Phong高光反射公式数学推演

概述

基础知识

向量投影

反射向量

应用

关于作者

Jsonco

相关文章

热门文章

热门问题

热门标签

等待解答

推荐达人