几何学——坐标系概括

坐标系简介

坐标系是描述物体或点的位置和方向的一种数学工具。它由坐标轴和原点组成，通常用于二维或三维空间中。

坐标轴是一条直线，其上有等距离的点，用来表示某个方向上的距离。在二维坐标系中，通常有两条垂直的坐标轴，即水平轴和垂直轴；在三维坐标系中，则需要增加一条竖直的轴。这些轴通常用 x、y 和 z 表示，并通过原点相交。

位置可以用一组数字（称为坐标）来描述。在二维坐标系中，每个点都有一个唯一的坐标，由它在水平轴和垂直轴上的位置确定。在三维坐标系中，每个点由它在三个轴上的位置确定。

坐标系不仅可以用来描述物体或点在空间中的位置和方向，还可以用于计算距离、角度、速度、加速度等物理量。它在数学、物理、工程、计算机科学等领域都有广泛应用。

坐标系是我们学习CG的基础，不管你是学习webgl还是shader，不可避免的就是学习各自的坐标系统。

笛卡尔坐标系

笛卡尔坐标系是一个用于描述平面或空间中点位置的数学工具。它由法国数学家笛卡尔（René Descartes）发明，并以他的名字命名。笛卡尔坐标系由两条互相垂直的直线，即x轴和y轴组成。

在平面直角坐标系中，每个点都可以通过一对有序实数(x, y)来表示。其中，x坐标表示点到y轴的水平距离；y坐标表示点到x轴的竖直距离。通常情况下，x轴向右为正方向，y轴向上为正方向。

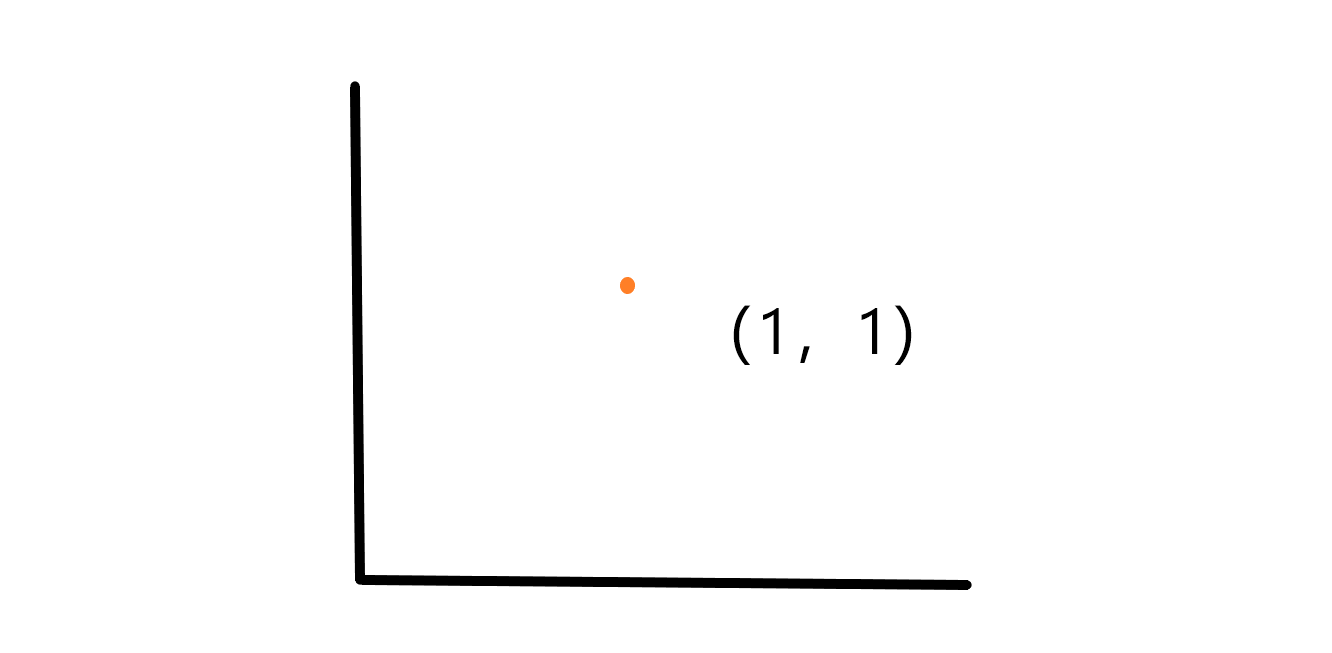
如上图所示我们想表示二维笛卡尔坐标系中的一个点P,可以用坐标（1,1）表示。

冰哥说：参考系不一样，最终造成二者的坐标表示内容也是不一样的，其实这点可以类推我们在图形学中讲到的物体坐标系。每个物体都有自己单独的坐标系，这样就会造成标准不统一，难以在统一的条件下进行控制多个物体。

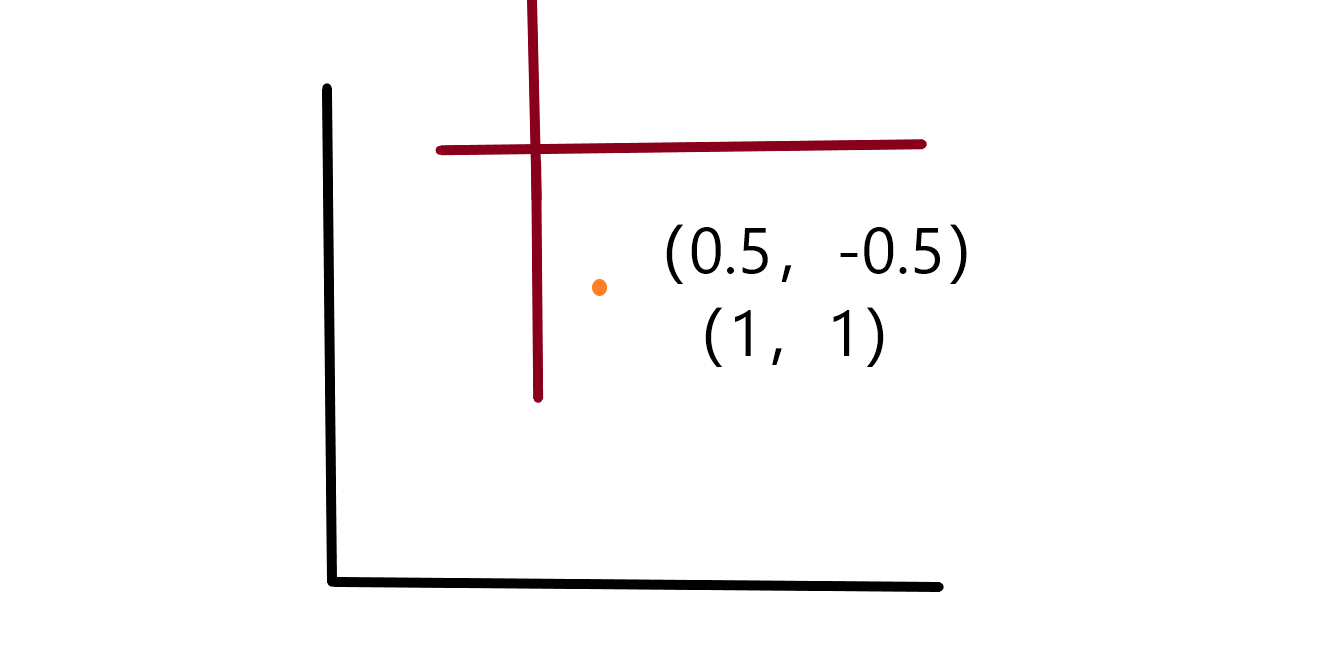
三维笛卡尔坐标系

在三维笛卡尔坐标系中，除了x轴和y轴之外，还有z轴。每个点可以用一个有序的实数三元组(x, y, z)来表示。x、y、z分别表示点到yz平面、xz平面和xy平面的距离。通常情况下，x轴向右为正方向，y轴向上为正方向，z轴向前为正方向。三维笛卡尔坐标系广泛应用于各种领域，如数学、物理、工程、计算机图形学等。在计算机图形学中，三维坐标系被用来描述三维物体的位置、大小和形状等属性，是实现三维渲染、动画和虚拟现实等技术的基础。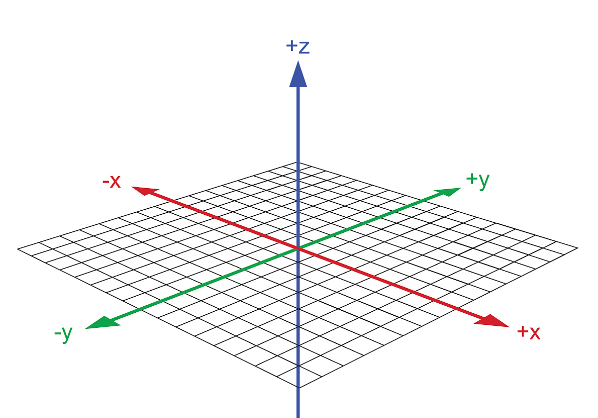

在线性代数中，三个轴（在一维和二维情况下分别为一个或两个）构成了我们所说的该坐标系的基础。基向量是一组线性独立的向量，它们以线性组合表示给定向量空间（坐标系）中的每个向量。更改基向量或更改坐标系是数学和图形管道中的常见操作。

冰哥说：基向量是一个矩阵或向量空间中的一组线性无关向量，可以通过它们来表示该空间中的任何向量。基向量集通常被称为基。在二维空间中，通常使用两个向量作为基向量。在三维空间中，则通常使用三个向量作为基向量。这些基向量被选为互相垂直且长度为1，因此它们可以用来描述空间中的任何向量。更一般地说，在n维向量空间中，需要n个线性无关的基向量才能表示该空间中的所有向量。这些基向量通常被写成列向量的形式，并排列成一个矩阵，这个矩阵就被称为基矩阵。

左手坐标系与右手坐标系

其实坐标系不复杂吧，但是由于CG发展，各种大佬就想形成商业垄断，所以采用不同的规格来形成自己的护城河，所以不同坐标系就分为了左手坐标系与右手坐标系。就这个有时让很多人感到迷惑。我们来看一下两个的一个大概区别。

为了区分这两种约定，我们将第一个坐标系称为左手坐标系，另一个坐标系称为右手坐标系。物理学家约翰·安布罗斯·弗莱明（John Ambrose Fleming）引入了左手和右手规则，以轻松区分这两种约定。

我们稍后将解释它与手有什么关系。但首先，让我们定义两个系统之间的区别。当 x 轴指向右侧，y 轴指向上方时，如果 z 轴指向远离你，则为左手坐标系。如果它指向你的方向，则为右手坐标系。

要记住每个坐标系的方向，请分别将 x、y 和 z 轴指定给拇指、食指和中指。这非常简单，因为这是我们自然展开手指的顺序。用左手和右手做这件事。然后将拇指向右定向，食指向上，中指将指示 z 轴的方向。

• 左手：远离你。
• 右手：朝你。

下面这张图我从网站上找的，你可以模仿这张图体验一下左右手坐标系。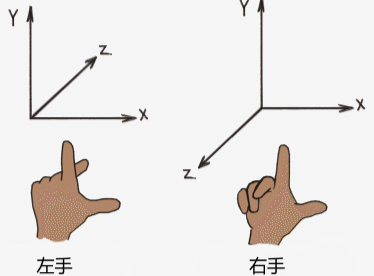

坐标系的惯用手性在从多边形面的边计算的法线方向中也起着重要作用。例如，如果方向为右手，则其折点按逆时针顺序指定的面将朝前。这将在渲染多边形对象的课程中解释。这个我们在WebGl中级课程中给大家讲解图形正面还是反面的时候提到过哈。这样可以提高webgl渲染效率。

webgl中级地址：https://www.bilibili.com/video/BV1nL411A7SM/?vd_source=01ae3fc576acbf5bd3e59f3307bb594f

物体坐标系（模型坐标系、身体坐标系、个体坐标系）

物体坐标系是三维空间中的一个坐标系，用于描述物体在三维空间中的位置和方向。通常情况下，物体坐标系的原点被定义为物体的质心或几何中心，并且其轴线会根据物体的形状而确定。物体坐标系是和特定物体相关联的坐标系。每个物体都有它们独立的坐标系。

冰哥说：很多同学就与物体坐标系和世界坐标系存在朦胧感。我结合实现的例子给大家举例子，比如此刻你要去北京天安门玩耍，高德导航会告诉你“向左转，向右转”。此时是以你个人为中心，也就等同于我们所讲的物体坐标系下的运动。有时候你行走的方向相反了，或者你偏移了很大角度，高德地图一般会提示你“您的方向偏移，请向南出发”此时他的意思就是在世界坐标系下进行的提醒，此刻你的目的地和你本身都是放在世界坐标系下去衡量的。

在计算机图形学中，物体坐标系通常被用来描述三维模型的位置、旋转和缩放状态。当需要对三维模型进行变换时，可以通过对其物体坐标系进行变换来实现。例如，通过对物体坐标系进行平移变换，可以将模型沿着某个轴线上移动一定距离；通过对物体坐标系进行旋转变换，可以将模型绕某个轴线旋转一定角度。

世界坐标系（全局坐标系、宇宙坐标系）

世界坐标系有很多名字，它类同于笛卡尔坐标系，只是它具有了物理属性，赋予了它在实际中的例子。上面我们提到其实每个物体都有自己的坐标系，但是实际我们在日常应用中，我们需要将各个坐标系进行统一化，在一个相同的约束下进行计算。所以世界坐标系就产生了，每个物体相对于世界坐标系都有自己的坐标。我们经常在小学学习地理的时候，老师告诉我们更具地球经纬度就可以获取到你的位置，所以人类根据这个基本原理，设定了WGS 84坐标系。学地理或者学GIS的同学一定对这个概念很清楚。实际上相对于地球来说，世界坐标系在球体的质心。

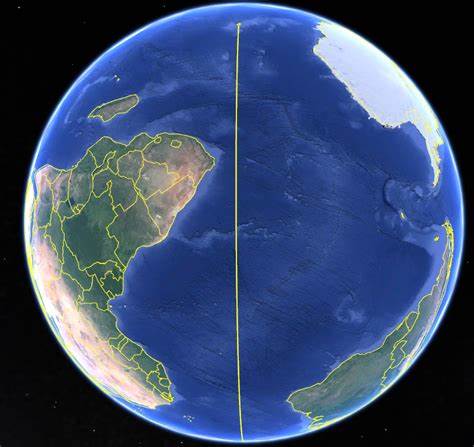
世界坐标系是一个特殊的坐标系，它建立了描述其他坐标系所需要的参考框架。从另一方面说，能够用世界坐标系描述其他坐标系的位置，而不能用更大的、外部的坐标系来描述世界坐标系。在世界坐标系里面的任何一个东西，我们都能用世界坐标表示。

惯性坐标系

惯性坐标系实际上是世界坐标系与物体坐标系的中间模块，为了方便二者转换，引入了一种新的坐标系，称作惯性坐标系。惯性坐标系的原点和物体坐标系的原点重合，惯性坐标系的轴平行于世界标系的轴。我们下面这张图，表示了三个坐标系的关系。橘黄色代表的是世界坐标系，蓝色代表的是惯性坐标系，深红色代表的是物体坐标系（原点在狗肚子....）

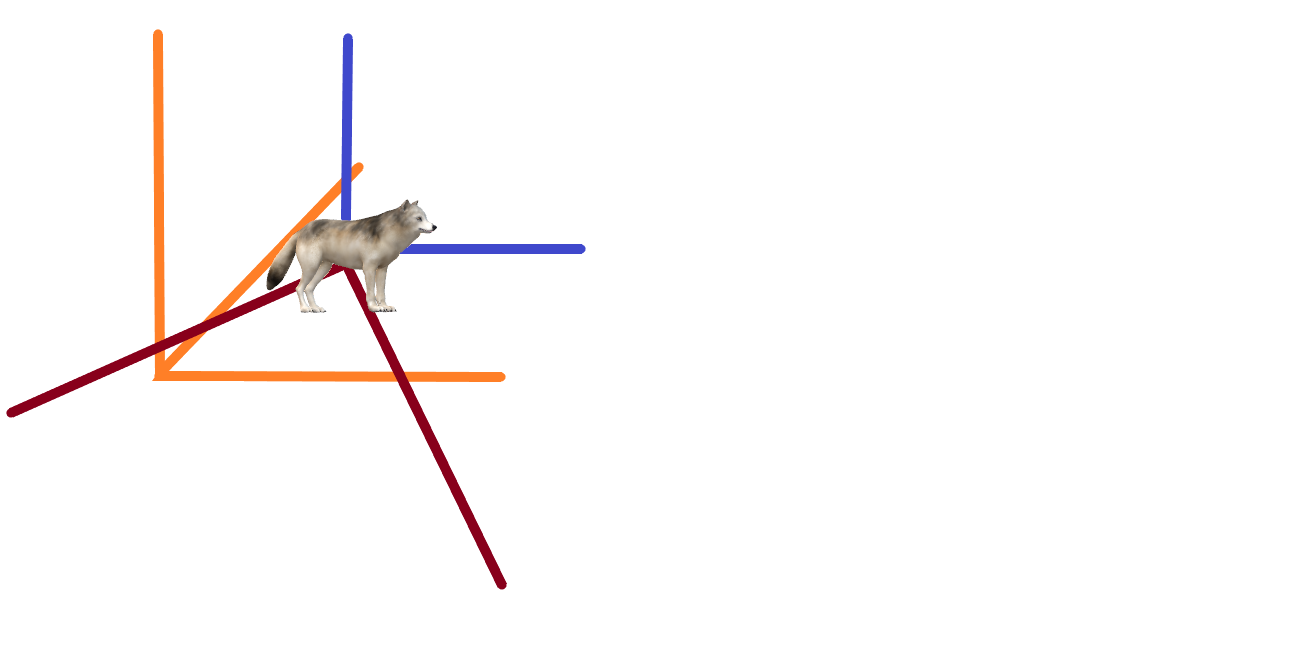
冰哥说：为什么要引入惯性坐标系呢?因为从物体标系转换到性标系只需旋转从性标系转换到界坐标系只需要平移。分开考虑着两件事比把它们合在一起容易得多。

嵌套坐标系

所谓的“嵌套坐标系”实际上是世界坐标系和物体坐标系的综合，比如举个例子，你仍然要去北京天安门游玩，在去的路上你相对地球来说，你的位置不断发生位移，这就属于在世界坐标系的坐标变换，在去天安门游玩的路上，你在路上吸了口烟，吐了口吐沫。这两个动作实际上是相对于你本身而言的，也就是物体坐标系。在实际程序开发中，我们应用嵌套坐标系的例子很多，比如我们在做人物奔跑、漫游、行走、坐下等连续式动画的时候。

相机坐标系

相机坐标系可以想象成你本人的观察视角。摄像机标系能被看作是一种特殊的“物体”坐标系，该“物体”坐标系就定义在摄像机的屏幕可视区域。摄像机坐标系中，摄像机在原点，x轴向右，z 轴向前(朝向屏幕内或摄像机方向)，y轴向上(不是世界的上方而是摄像机本身的上方)。

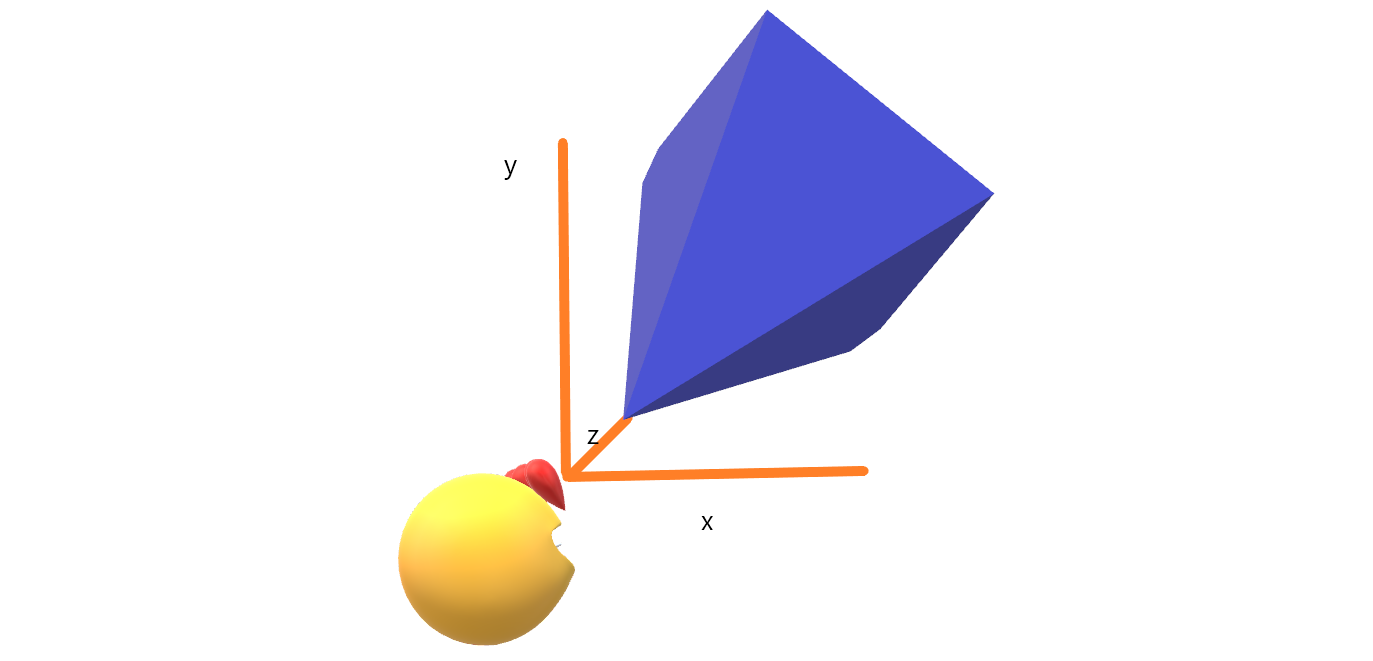
投影坐标系（裁减坐标系）

投影坐标系，也称为裁减坐标系，是计算机图形学中一个重要的概念。在三维图形学中，我们通常使用三维对象描述场景。然而，在实际应用中，我们需要在二维屏幕上显示这些场景。因此，必须将三维场景中的点映射到二维投影平面上。这个过程就需要用到投影坐标系。

投影坐标系一般分为正交投影和透视投影。

屏幕坐标系

屏幕坐标系是计算机图形学中用于表示屏幕上的像素位置的坐标系。它通常是一个以左上角为原点（0,0）的二维直角坐标系，其中水平方向向右为正方向，垂直方向向下为正方向。在屏幕坐标系中，每个像素都可以由其 x 和 y 坐标确定。例如，屏幕上的某个像素可能具有坐标 (100, 200)，这意味着它距离屏幕左侧100个像素，距离屏幕顶部200个像素。

坐标系转换

其实坐标系转换是同一个事物在不同坐标系下的表现形式。两个不同坐标的转换过程被称为“坐标系转换”。我们在webgl高级中给大家详细的介绍了其推导过程。

总结

这章节的内容实际上也是非常基础的，但是他往往经常出现在我们看CG相关的文献资料中，当然这样是我们学习几何学的基础。如果你想在实践中更多的理解，建议你看看我webgl高级课程，介绍了webgl渲染流水线以及坐标变换的理论知识。

webgl高级地址：https://www.bilibili.com/video/BV1HU4y1e7JS/?vd_source=01ae3fc576acbf5bd3e59f3307bb594f

坚持下去，一定会有很大收获，下期见！