几何学——点、向量和法线

线性代数

我们在webgl课程中给大家讲到了一定的数学知识，其实他并不是完整的，我们在很多应用实例中了解到，其实很多时候我们也可以不用线性代数，也可以实现。其实我们在之前课程中也定义过线性代数的“下里巴人”定义：线性代数只不过是数学家定义的牢笼。-（没错冰哥我说的）为什么这个牢笼不是你定义的呢，因为你不是牛逼的数学家，他们就是想制定一个规格化的数据组织标准，方便后面的数学推导和运算，恰巧的是我们计算机很喜欢这种规格化的数据格式，所以它被广泛应用到计算机图形学里面咯。

没事的哥们可以去读读这本书，我记得考研时候就是读的这本。此外我推荐下考研李永乐老师的课程，反正我很喜欢。

点

点是最基础的几何形状了吧。点是三维空间中的一个位置。在本课中，我们将图形学中诠释它本身的意义。我们可以通过下面方式表示一个点

vec3 a= vec3(0.,0.,1.);

上面函数用来表示一个在z轴上面的点。

向量

向量又称为矢量，具体定义我们不再过多介绍。但向量可以在CG中可以用数字数组表示。这个数字数组可以假定任何所需的长度，有时也称为数学中的元组。

冰哥说：元组是数学中的一个概念，它指的是有序数对或者有序 n 元组。元组的形式可以表示为 (a1, a2, ..., an)，其中每个元素ai 可以是任意数值类型，也可以是其他数据类型。在数学中，元组通常用于描述多个变量之间的关系或者属性。例如，一个二维平面上的点可以表示为一个含有两个元素的元组 (x, y)。

如果我们想具体说明向量的大小，我们可以选择说 n 元组，其中 n 表示向量中元素的数量。下面是具有4个元素的向量示例：

$$ P = （a， b， c， d） 其中 a、b、c、d是实数。 $$

在计算机图形学中，向量可以表示空间中的位置或方向。CG中提供了很多方法来操控这些向量，变换这些向量的方法我们称为线性变换。我们将在后面的部分中花费更多时间才一起研究这块内容。

冰哥说：线性变换是指一种将一个向量空间中的向量映射到另一个向量空间中的操作。线性变换在向量空间中有着广泛的应用，包括矩阵乘法、旋转、缩放、投影等等。

向量通常表示三维空间中的一个方向。三维点和向量相似，因为它们都由上面提到的元组表示。

$$ P = （x， y， x）同样，其中 （x， y， z） 是实数。 $$

向量或点不一定局限于我们在CG中的使用。对他们来说，向量可以是任意的，甚至是无限的（这意味着它可以包含任意数量的数字）。

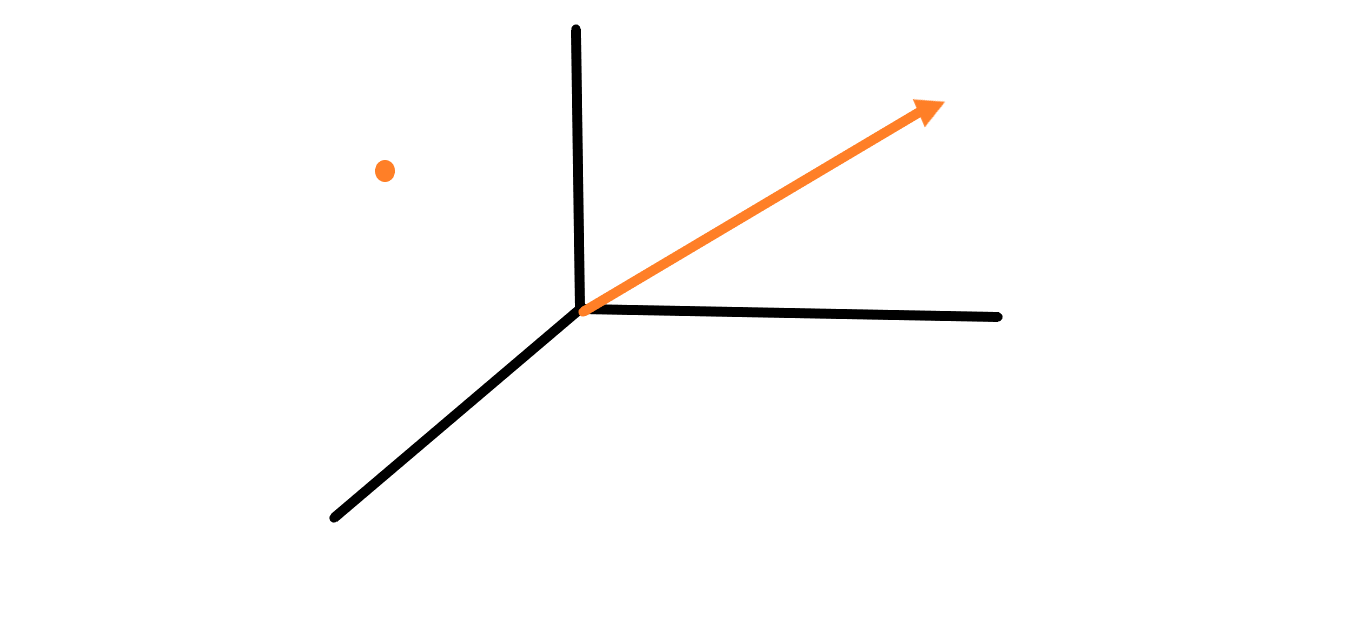
有时为了数学上计算方便，有必要添加第四个元素。这块我在之前webgl课程里面专门给大家分析过，数学具体为什么这样去做。下面给出了具有齐次坐标的点的示例：

$$ P_H=（x， y， z， w） $$

在本文档的后面会再次给大家详细解释其内容。

行向量与列向量

行向量和列向量是矩阵的特殊形式，它们分别只有一行和一列。

行向量

行向量是一个 1 × n 的矩阵，其中 n 是元素的数量。例如：

$$ A = [a₁, a₂, ..., aₙ] $$

列向量

列向量是一个 n × 1 的矩阵，其中 n 是元素的数量。例如：

$$ b = \left[\begin{matrix}b1\\ b2\\b3\end{matrix}\right] $$

冰哥说：行向量和列向量二者可以通过转置进行互相转换，不同的图形引擎API中转换，使用的也是不一样的，比如directX就是行向量，opengl就是列向量。不同的作者使用不同的约定。当使用别人的公式或源代码时，切记要检查使用的是行向量还是列向量如果某书使用列向量，那么用它的公式和本书的公式对比时要首先进行转换。例如，乘法vABC仅当v是行向量时才合法，使用列向量则对应的乘法为 CBAv。后面我们给大家在推导向量和矩阵乘法的时候就能清晰的理解这一点。

法线

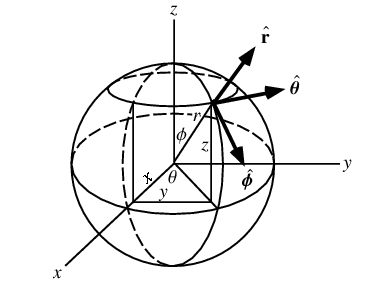
在计算机图形学中，法线（Normal）是指垂直于曲面或多边形表面的向量。法线通常被用来计算光照和阴影，以及决定物体表面如何反射光线。

对于平面图形，法线向量垂直于平面。对于曲面图形，法线向量在每个点都沿着曲面的切线方向垂直于曲面。法线可以通过数学方法计算出来，也可以在计算机中使用渲染器自动生成。在3D建模软件中，用户可以手动编辑法线来调整曲面的光滑度和外观。在计算机图形学中，法线是一个非常重要的概念，在三维建模、游戏开发、虚拟现实等领域都得到了广泛应用。

其实向量是一个基础概念，法线可以看做是向量的一个具体应用。但是法线有自己的独特的特性，后面我们具体讨论。

总结

第一章结束了，后面我们会慢慢深入讨论后续的内容，也请具体结合我B站课程在具体工程实践中不断加强自身的练习。