shader 图形学 几何

根据SDF绘制更多的三维形状（持续更新）

发布于 2023-04-20 14:23:57

背景

三维SDF，全称为三维有符号距离场（Signed Distance Field），是一种用于表示三维模型的方法。它将每个点到最近模型表面的距离作为该点的值，并根据其位置与模型表面的关系（在内部或外部）对其进行符号化处理。

三维SDF常用于计算机图形学、虚拟现实和机器人视觉等领域，因为它可以提供高效和准确的几何描述。通过使用三维SDF，我们可以执行空间中点的快速查询，以确定它们是否在模型内部或外部，以及它们到模型表面的最短距离。

三维SDF是由二维SDF推广而来，其中二维SDF用于表示二维形状。三维SDF可以通过多种方式计算，例如离散方法、隐式方法和显式方法。离散方法基于网格表示模型，并计算每个网格顶点的距离值。隐式方法则将距离场作为一个解析函数表示，而显式方法则基于已知的距离值进行插值。

现实中三维形状.png

绘制多个三维SDf

前言

这节我们讲解绘制各种不同的三维SDF，此节内容比较多，并且持续更新，因为三维世界中具有各种不一样的三维形状，我们尽可能多给大家描述，下面是我们常见的三维SDF形状。

绘制三维SDF.png

前情回顾

在绘制多个三维SDF之前，我们将上次讲解的光线追踪整个代码进行规整如下，如果你忘记了该部分理论，建议回顾下之前的内容：

光纤追踪.png

// Author: ice
// Title: 光线追踪

#ifdef GL_ES
precision mediump float;
#endif
#define MAX_ITERATIO_NNUMBER 255
#define MIN_DISTANCE 0.001
#define START_POSITION 0.
#define END_POSITION 100.
uniform vec2 u_resolution;
uniform float u_time;
mat2 r2d(float a) {
    float c = cos(a), s = sin(a);
    return mat2(
        c, s, // column 1
        -s, c // column 2
    );
}
float sdfPlane(vec3 p){
    return p.y;
}
float sdfSphere(vec3 p,vec3 move, float r){
    return length(p-move)-r;
}
float getDistance(vec3 p, float r){
  
    float plane =sdfPlane(p);
    float sphere =sdfSphere(p,vec3(0.,2.,-6.),1.540);
    return min(plane,sphere) ;
}

//法线函数
vec3 getNormal(vec3 p,float r){
    float e = 0.0001;
    
    vec3 n = normalize(
        vec3(
        getDistance(p+vec3(e,0,0),r)-getDistance(p-vec3(e,0,0),r),
        getDistance(p+vec3(0,e,0),r)-getDistance(p-vec3(0,e,0),r),
        getDistance(p+vec3(0,0,e),r)-getDistance(p-vec3(0,0,e),r)
            
            ));
    return n;
}

float rayMaching(vec3 eyedrection,vec3 eyePosition){
    float d = START_POSITION;
    
    for(int i = 0;i<MAX_ITERATIO_NNUMBER;i++){
        vec3 p =eyePosition+ d* eyedrection;
      
        float newd  = getDistance(p ,2.);
        d+=newd;
        if(newd<MIN_DISTANCE||d>END_POSITION){
            break;
        }
    }
     return d ;
}


void main() {
    vec2 uv = (gl_FragCoord.xy*2.-u_resolution.xy)/min(u_resolution.x,u_resolution.y);
    vec3 col = vec3(0.);
    vec3 eyeposition  = vec3(0, 5,1.);
    vec3 eyedrection  =normalize( vec3(uv,-1.));
    float d = rayMaching(eyedrection,eyeposition);
    

    //光线检测后的坐标p
    vec3  p = eyeposition+eyedrection*d;
    vec3 lightPosition = vec3(0, 5, 6);
    //围绕着xz轴旋转
    lightPosition.xz *=r2d(u_time*0.5) ;
    vec3 lightDirection = normalize(lightPosition-p);
    vec3 n = getNormal(p,2.);
    float diff =clamp(dot(n, lightDirection), 0., 1.);
    
    //创造阴影
    float shdowd = rayMaching(lightDirection,p+n*0.01);
    if(shdowd<length(lightPosition-p)){diff *= 0.1;} 
    col = vec3(diff );
    col = pow(col, vec3(3.));    
    gl_FragColor = vec4(col,1.0);
}

线段

线段实际上和二维的是一样的，具体逻辑可以参考之前文章二维线段SDF编写。具体代码如下所示：

float sdfLine(vec3 p, vec3 a, vec3 b ,float r){
    vec3 ap = p-a;
    vec3 ab = b-a;
    float k  =   clamp( dot(ap,ab)/dot(ab,ab), 0.0, 1.0 );
    float d = length(ap-k*ab)-r;
    return d;

}

圆环

圆环SDF.png

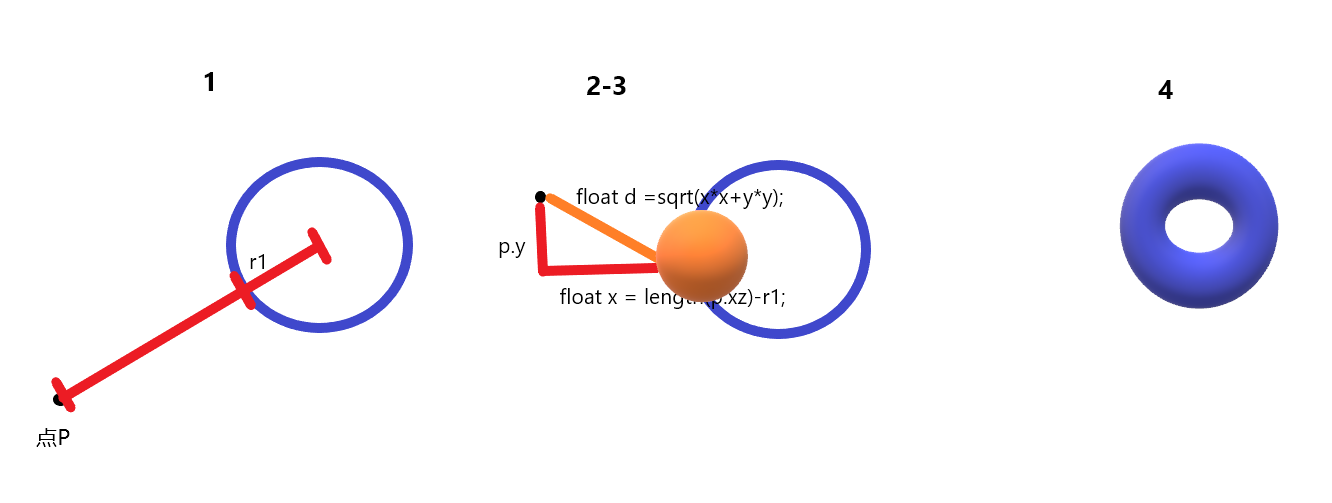
（1）假设空间xz平面上存在一点P，现在xz平面上绘制一个圆形.其SDF公式我们应该熟知了：

   float x = length(p.xz)-r1;

注：我们假设的是xz平面，就是底面，你也可以假设其他坐标面为基准。

（2）圆形画成之后，我们假设要在这个圆形里面再套一个小圆球，并且小圆形围绕着大圆形旋转。最后形成我们的圆环。所以我们这一步的工作主要是探讨如何生成小圆球。

float d = 空间站P点到小圆球距离-r2

（3）那么空间中点P到小圆球的距离如何计算呢？

我们在步骤（1）中求的值是P点在xz平面下的投影值，也就是P点到小圆球中心的距离，又已知P的y值构成勾股定理，所以可以求得P点到“小圆球中心距离”

float y = p.y;
float d =sqrt(x*x+y*y);

(4)最后我们要表示小圆球的SDF，必须还得减去小圆球的半径r2

float y = p.y;
float d =sqrt(x*x+y*y)-r2;

正方体

正方体是我们在二维下长方形的拓展规则，具体可以参照我们对于二维SDF的理解。其实现代码如下所示：

float sdfBox( vec3 p, vec3 b )
{
  vec3 q = abs(p) - b;
  return length(max(q,0.0)) + min(max(q.x,max(q.y,q.z)),0.0);
}

如果我们想做圆角边的正方体，在上述标准正方体的基础上再减去一个常数，这个常数就是圆角的半径。代码如下所示：

float sdfRoundBox( vec3 p, vec3 b, float r )
{
  vec3 q = abs(p) - b;
  return length(max(q,0.0)) + min(max(q.x,max(q.y,q.z)),0.0) - r;
}

其实原因也很简单，你可以这样直观的理解：减去r类似我们的球体，说明在顶点处分别加了几个球，最后球和我们正方体做了一个融合。

圆柱

float sdfCylinde(vec3 p, vec3 a, vec3 b ,float r){
    vec3 ab = b-a;
    vec3 ap = p-a;
    float k = dot(ap,ab)/dot(ab,ab);
    float d = length(ap-k*ab)-r;
    float y = (abs(k-.5)-.5)*length(ab);
    float e = length(max(vec2(d,y),0.));
    float i = min(max(d,y),0.);
    return i+e;
}

全部代码

// Author: ice
// Title: 绘制多个3D图形

#ifdef GL_ES
precision mediump float;
#endif
#define MAX_ITERATIO_NNUMBER 255
#define MIN_DISTANCE 0.001
#define START_POSITION 0.
#define END_POSITION 100.
uniform vec2 u_resolution;
uniform float u_time;
mat2 r2d(float a) {
    float c = cos(a), s = sin(a);
    return mat2(
        c, s, 
        -s, c 
    );
}
float sdfLine(vec3 p, vec3 a, vec3 b ,float r){
    vec3 ap = p-a;
    vec3 ab = b-a;

    float k  =clamp( dot(ap,ab)/dot(ab,ab), 0.0, 1.0 );
    float d = length(ap-k*ab)-r;
    return d;

}
float sdfRing(vec3 p,float r1,float r2){
    float x = length(p.xz)-r1;
    float y = p.y;
    float d =sqrt(x*x+y*y) -r2;
    return d;
}
float sdfBox(vec3 p,float b){
   vec3 q = abs(p) - b;
  return length(max(q,0.0))-.5 ;
   
}
float sdfCylinde(vec3 p, vec3 a, vec3 b ,float r){
    vec3 ab = b-a;
    vec3 ap = p-a;
    float k = dot(ap,ab)/dot(ab,ab);
    float d = length(ap-k*ab)-r;
    float y = (abs(k-.5)-.5)*length(ab);
    float e = length(max(vec2(d,y),0.));
    float i = min(max(d,y),0.);
    return i+e;
}
float sdfSphere(vec3 p, float r){
    float d = length(p)-r;
    return d; 
}
float getDistance(vec3 p, float r){
  
    float plane = p.y-0.;
    float line =sdfLine(p-vec3(0.3),vec3(0,1,1),vec3(0,1,2),.3);
    float d = min(line,plane) ;
    float cylinde=sdfCylinde(p-vec3(-.6),vec3(0,1,1),vec3(0,3,1),.2);
    d = min(cylinde, d ) ;
    float box = sdfBox(p-vec3(2.),.3); 
    d = min(box, d ) ;
    float ring = sdfRing(p+vec3(4.,-1.,1.),1.5,.5);
    d = min(ring, d ) ;
    float sdfsphere =  sdfSphere(p-vec3(1.),0.656);
    d= min(sdfsphere,d);
    return d;
}


vec3 getNormal(vec3 p,float r){
    float e = 0.0001;
    

    vec3 n = normalize(
        vec3(
            getDistance(p+vec3(e,0,0),r)-getDistance(p-vec3(e,0,0),r),
        getDistance(p+vec3(0,e,0),r)-getDistance(p-vec3(0,e,0),r),
        getDistance(p+vec3(0,0,e),r)-getDistance(p-vec3(0,0,e),r)
            
            ));
    return n;

}

float rayMaching(vec3 eyedrection,vec3 eyePosition){
    float d = START_POSITION;
    

    for(int i = 0;i<MAX_ITERATIO_NNUMBER;i++){
        vec3 p =eyePosition+ d* eyedrection;
      
        float newd  = getDistance(p ,2.);
        d+=newd;
        if(newd<MIN_DISTANCE||d>END_POSITION){
            break;
        }
    }
     return d ;

}

void main() {
    vec2 uv = (gl_FragCoord.xy*2.-u_resolution.xy)/min(u_resolution.x,u_resolution.y);
    vec3 col = vec3(0.);
    vec3 eyeposition  = vec3(0, 4,6.);
    vec3 eyedrection  =normalize( vec3(uv,-1.));
    float d = rayMaching(eyedrection,eyeposition);

    //光线检测后的坐标p
    vec3  p = eyeposition+eyedrection*d;
        vec3 lightPosition = vec3(0, 5, 6);
        lightPosition.xz *=r2d(u_time*0.5) ;
       vec3 lightDirection = normalize(lightPosition-p);
        vec3 n = getNormal(p,2.);
     
        float diff =clamp(dot(n, lightDirection), 0., 1.);
     float shdowd = rayMaching(lightDirection,p+n*0.01);
    if(shdowd<length(lightPosition-p)){diff *= 0.1;} 
    col = vec3(diff );
    col = pow(col, vec3(.4545));    
    gl_FragColor = vec4(col,1.0);

}

绘制盒子

接下来我们使用光线追踪实现三维盒子的绘制功能。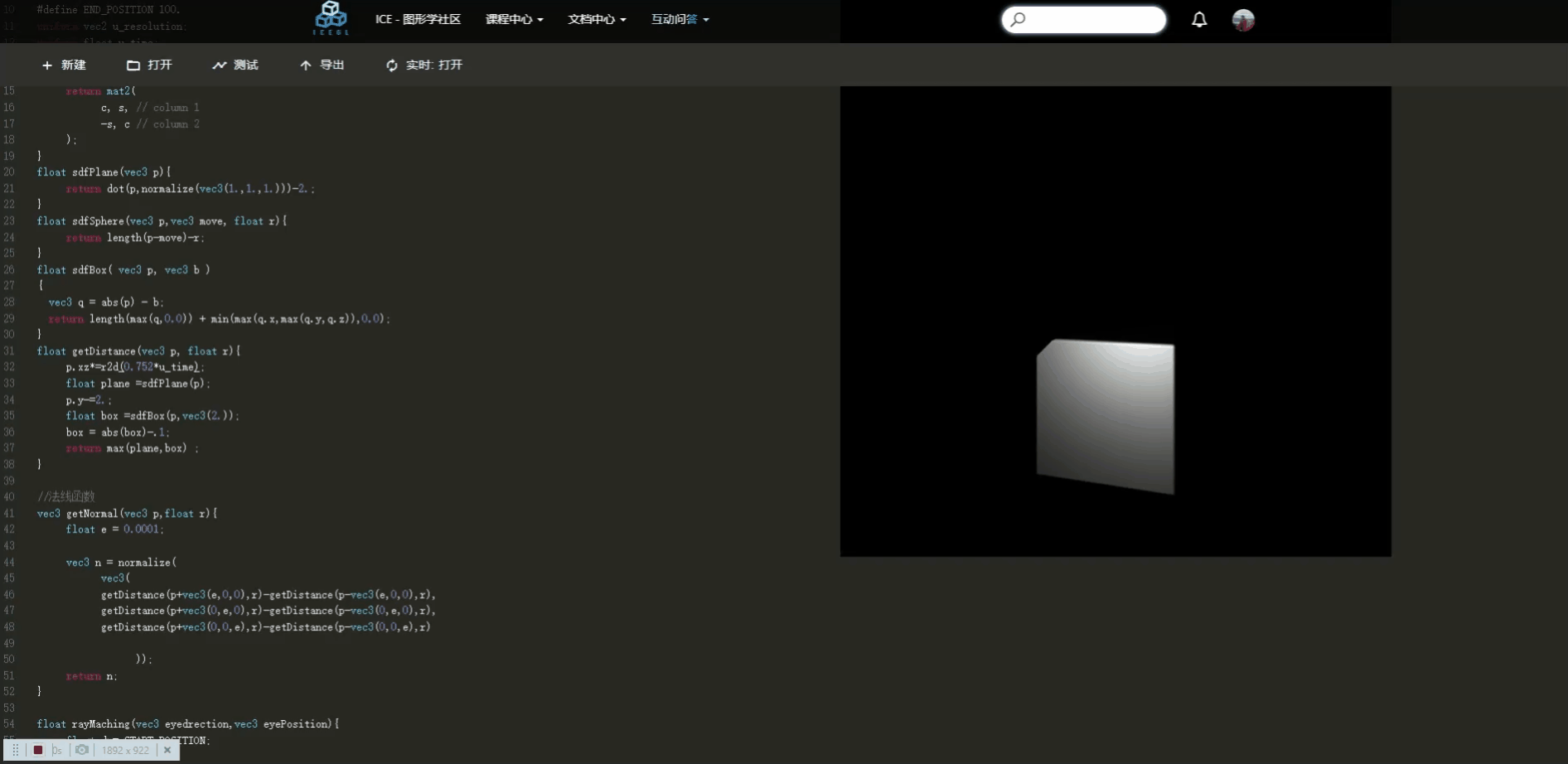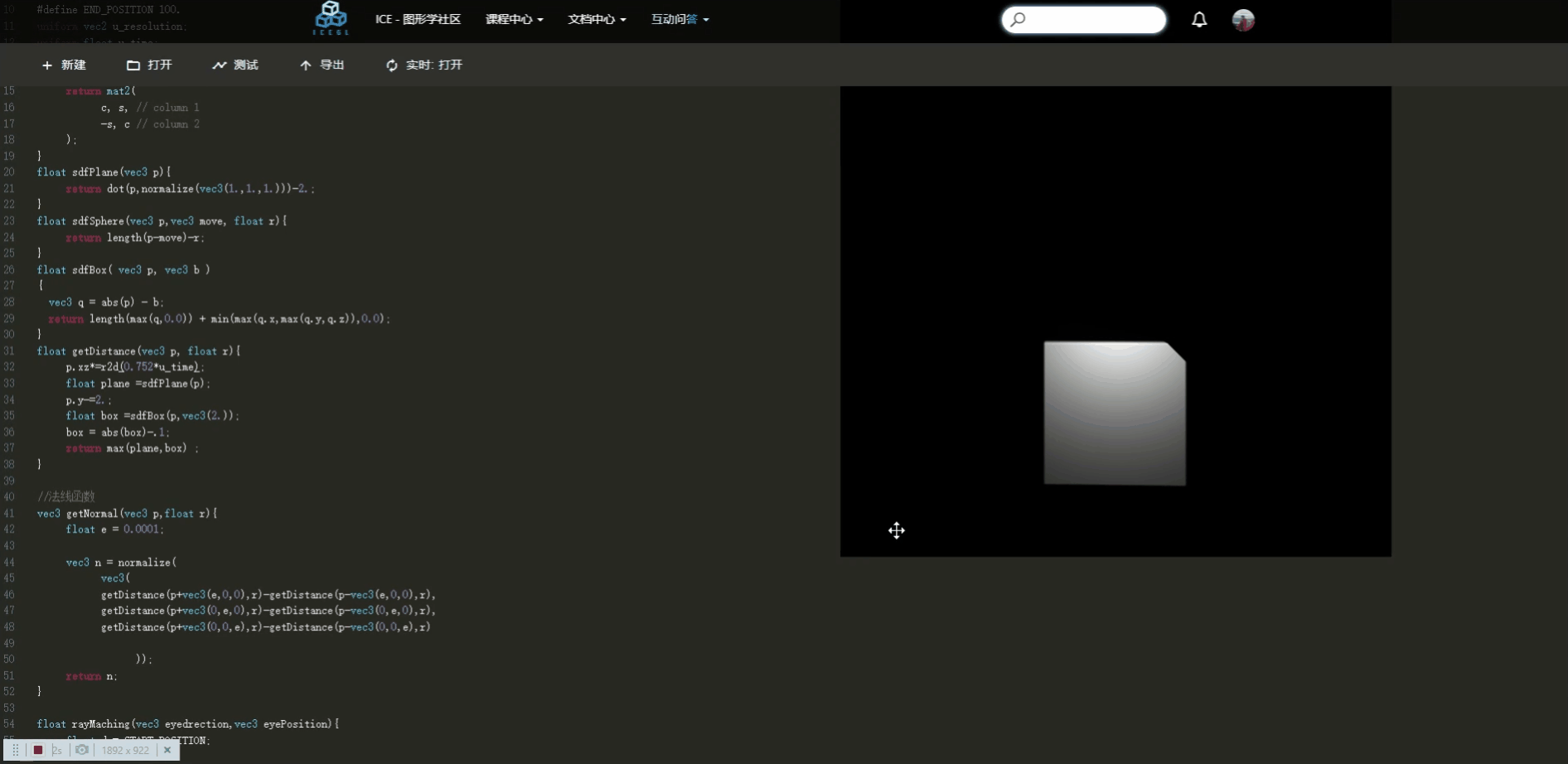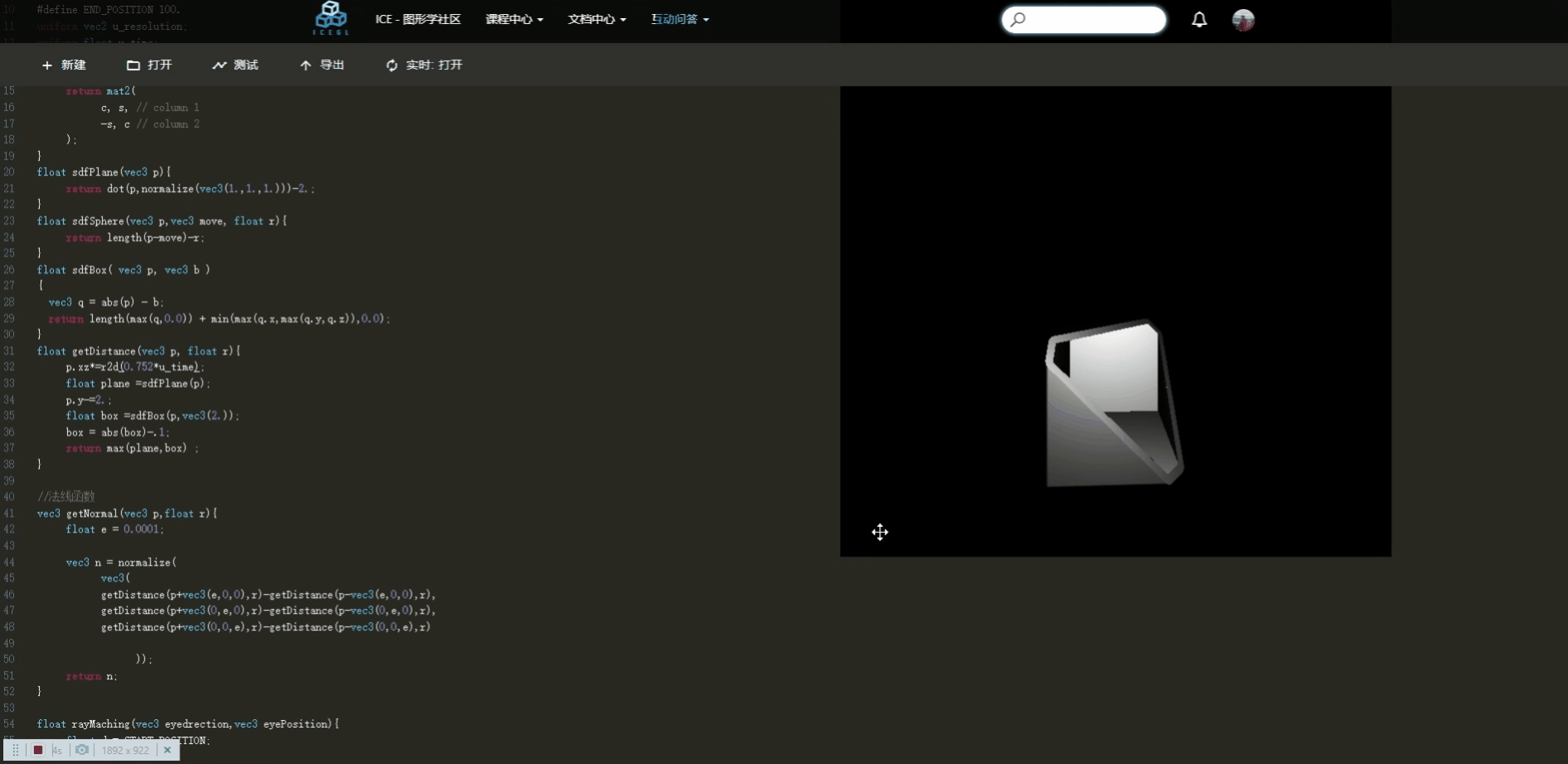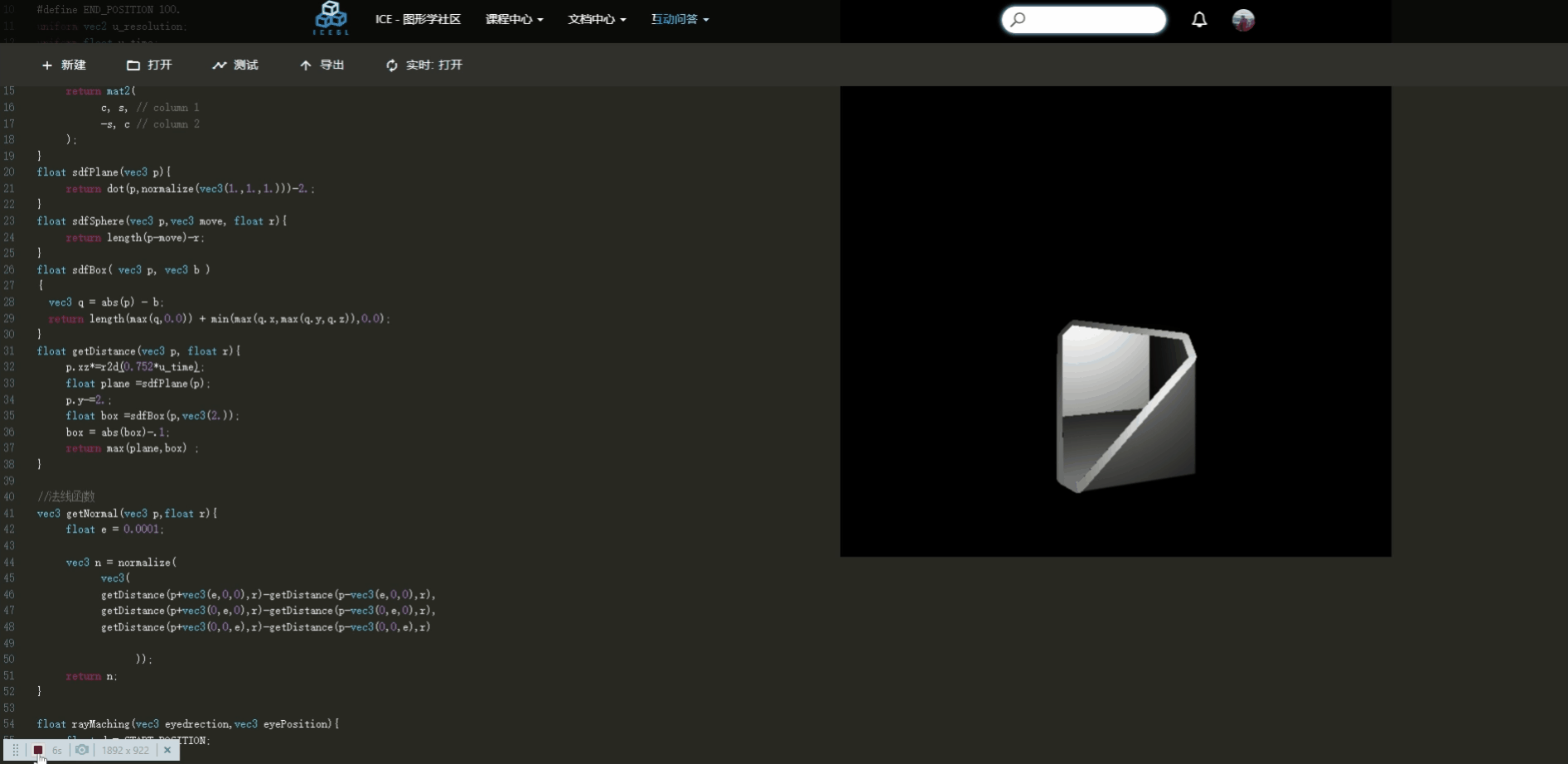
盒子.gif

冰哥说：“盒子”本质理论是里外都是空的。这点尤为关键，我们前面了解sdf理论，我们根据距离判断，几何体的外面length>0，几何体的内部length<0。如果要形成“盒子”结构，我们只需要在使其在某个范围内length>0，其余部分小于0即可。所以我们随即想到了abs函数。具体看下面代码的解释。

首先，这段代码是对Plane平面的修改：

//之前的代码是这样的
float sdfPlane(vec3 p){
    return p.y-2.;
}
//现在的代码是这样的
float sdfPlane(vec3 p){
    return dot(p,normalize(vec3(0.,1.,0.)))-2.;
}

上述代码结果是一样的，我们详细解释下dot(p,normalize(vec3(0.,1.,0.)))代码的意义，因为后续我们根据此技巧，生成更多有意思的图形。dot函数是两个向量的点乘，其几何及意义是可以看作是一个向量到另一个向量的投影，这点我们在图形学几何矢量计算一课中讲解到。dot函数转换成数乘结果如下：

$$ N \cdot M = N.x * M.x + N.y * M.y + N.z * M.z $$

你可以根据上述公式求得dot(p,normalize(vec3(0.,1.,0.)))=p.y。

之后，我们继续使用我们abs函数，abs函数我们在中级课程中也给大家安排了，等同于-1<box<1,所以就造成了盒子的效果。

   box = abs(box)-.1;

最后，我们将使用max函数获取的是plane与box几何图形的交集。具体可以查看关于max函数用法

float getDistance(vec3 p, float r){
    //模型旋转
    p.xz*=r2d(0.752);
     //绘制平面
    float plane =sdfPlane(p);
    p.y-=2.;
    float box =sdfBox(p,vec3(2.));
    box = abs(box)-.1;
    return max(plane,box) ;
}

拓展应用

我们来试试min函数效果，此时你可以回忆一下min函数使用场景。min函数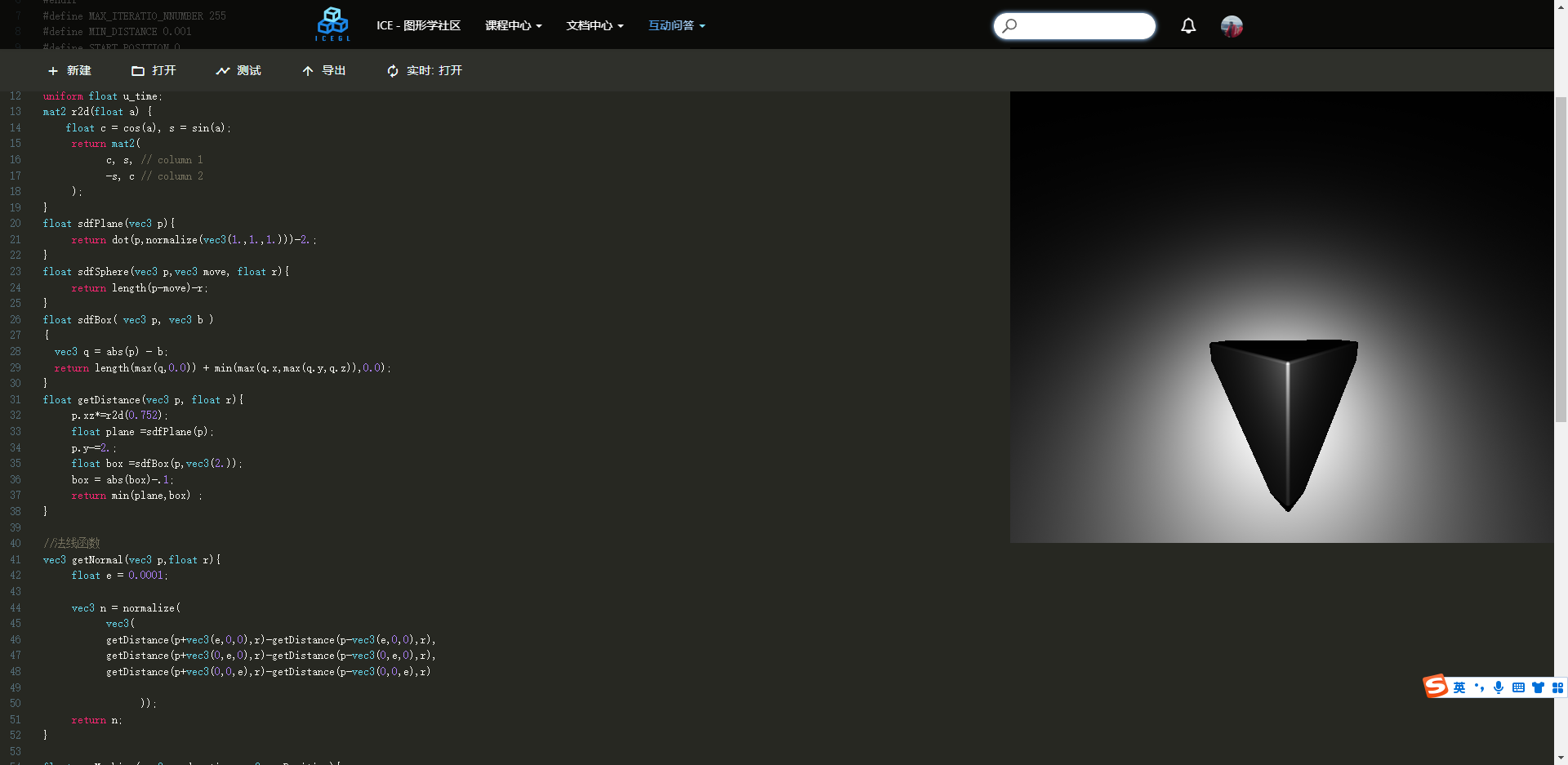
min函数.png

sin函数制造波浪线.png

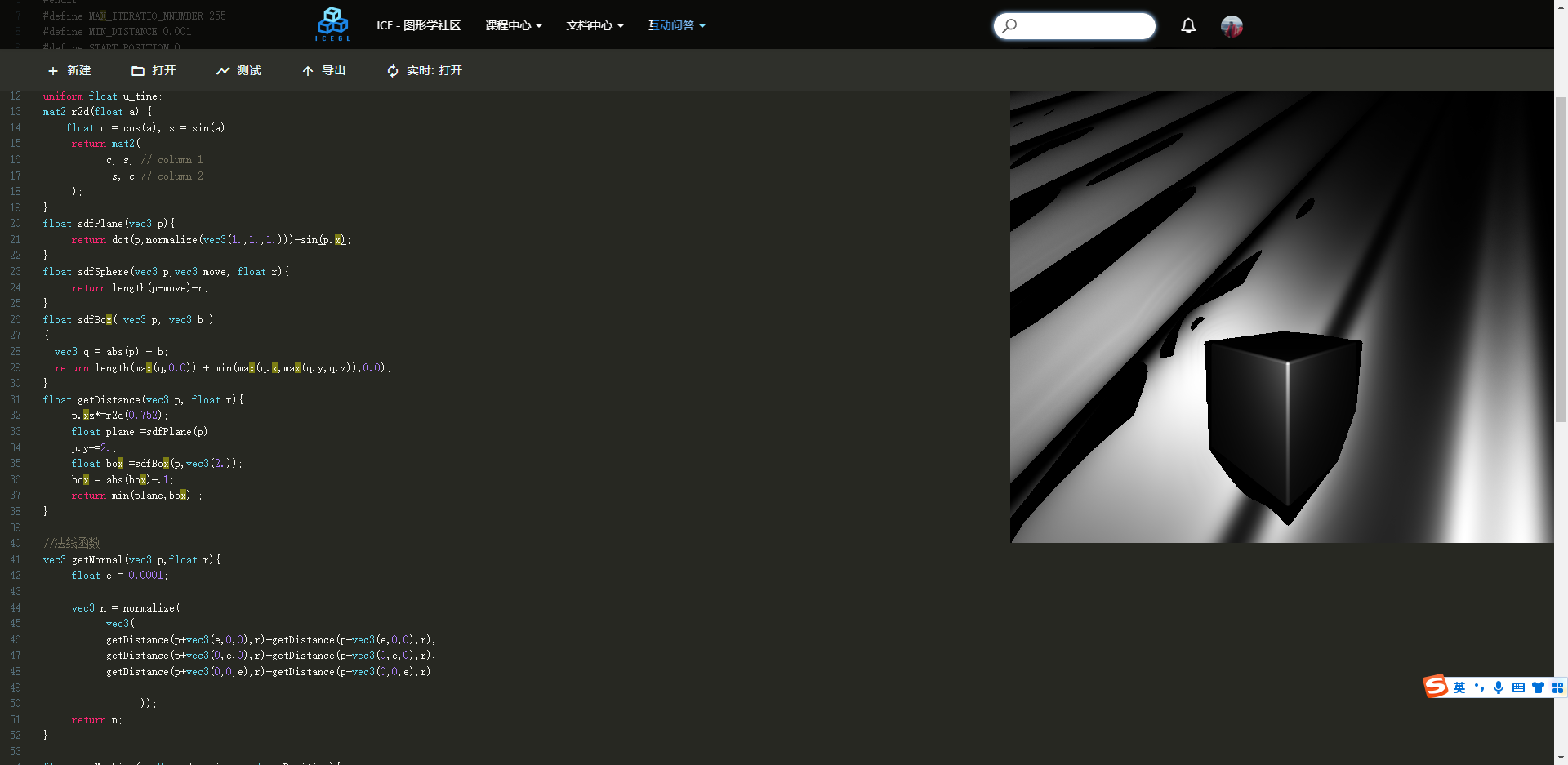
float getDistance(vec3 p, float r){
    p.xz*=r2d(0.752);
    float plane =sdfPlane(p);
    p.y-=2.;
    float box =sdfBox(p,vec3(2.));
    box = abs(box)-.1;
    return min(plane,box) ;
}

关于绘制盒子全部代码

// Author: ice
// Title: 绘制盒子

#ifdef GL_ES
precision mediump float;
#endif
#define MAX_ITERATIO_NNUMBER 255
#define MIN_DISTANCE 0.001
#define START_POSITION 0.
#define END_POSITION 100.
uniform vec2 u_resolution;
uniform float u_time;
mat2 r2d(float a) {
    float c = cos(a), s = sin(a);
    return mat2(
        c, s, // column 1
        -s, c // column 2
    );
}
float sdfPlane(vec3 p){
    return dot(p,normalize(vec3(1.,1.,1.)))-2.;
}
float sdfSphere(vec3 p,vec3 move, float r){
    return length(p-move)-r;
}
float sdfBox( vec3 p, vec3 b )
{
  vec3 q = abs(p) - b;
  return length(max(q,0.0)) + min(max(q.x,max(q.y,q.z)),0.0);
}
float getDistance(vec3 p, float r){
    p.xz*=r2d(0.752);
    float plane =sdfPlane(p);
    p.y-=2.;
    float box =sdfBox(p,vec3(2.));
    box = abs(box)-.1;
    return max(plane,box) ;
}

//法线函数
vec3 getNormal(vec3 p,float r){
    float e = 0.0001;
    
    vec3 n = normalize(
        vec3(
        getDistance(p+vec3(e,0,0),r)-getDistance(p-vec3(e,0,0),r),
        getDistance(p+vec3(0,e,0),r)-getDistance(p-vec3(0,e,0),r),
        getDistance(p+vec3(0,0,e),r)-getDistance(p-vec3(0,0,e),r)
            
            ));
    return n;
}

float rayMaching(vec3 eyedrection,vec3 eyePosition){
    float d = START_POSITION;
    
    for(int i = 0;i<MAX_ITERATIO_NNUMBER;i++){
        vec3 p =eyePosition+ d* eyedrection;
      
        float newd  = getDistance(p ,2.);
        d+=newd;
        if(newd<MIN_DISTANCE||d>END_POSITION){
            break;
        }
    }
     return d ;
}


void main() {
    vec2 uv = (gl_FragCoord.xy*2.-u_resolution.xy)/min(u_resolution.x,u_resolution.y);
    vec3 col = vec3(0.);
    vec3 eyeposition  = vec3(0, 6,10.);
    vec3 eyedrection  =normalize( vec3(uv,-1.));
  
    float d = rayMaching(eyedrection,eyeposition);
    

    //光线检测后的坐标p
    vec3  p = eyeposition+eyedrection*d;
    vec3 lightPosition = vec3(0, 5, 6);
    //围绕着xz轴旋转
    lightPosition.xz *=r2d(u_time*0.) ;
    vec3 lightDirection = normalize(lightPosition-p);
    vec3 n = getNormal(p,2.);
    float diff =clamp(dot(n, lightDirection), 0., 1.);
    
    //创造阴影
    float shdowd = rayMaching(lightDirection,p+n*0.01);
    if(shdowd<length(lightPosition-p)){diff *= 0.1;} 
    col = vec3(diff );
    col = pow(col, vec3(3.));    
    gl_FragColor = vec4(col,1.0);
}

绘制旗帜

假设此刻我想将plane平面进行改造，比如我们想构造出惊人的波浪线，如何改造呢？波浪线等于sin函数或者cos函数。效果如下图所示：
sin函数制造波浪线.png

不完美.png

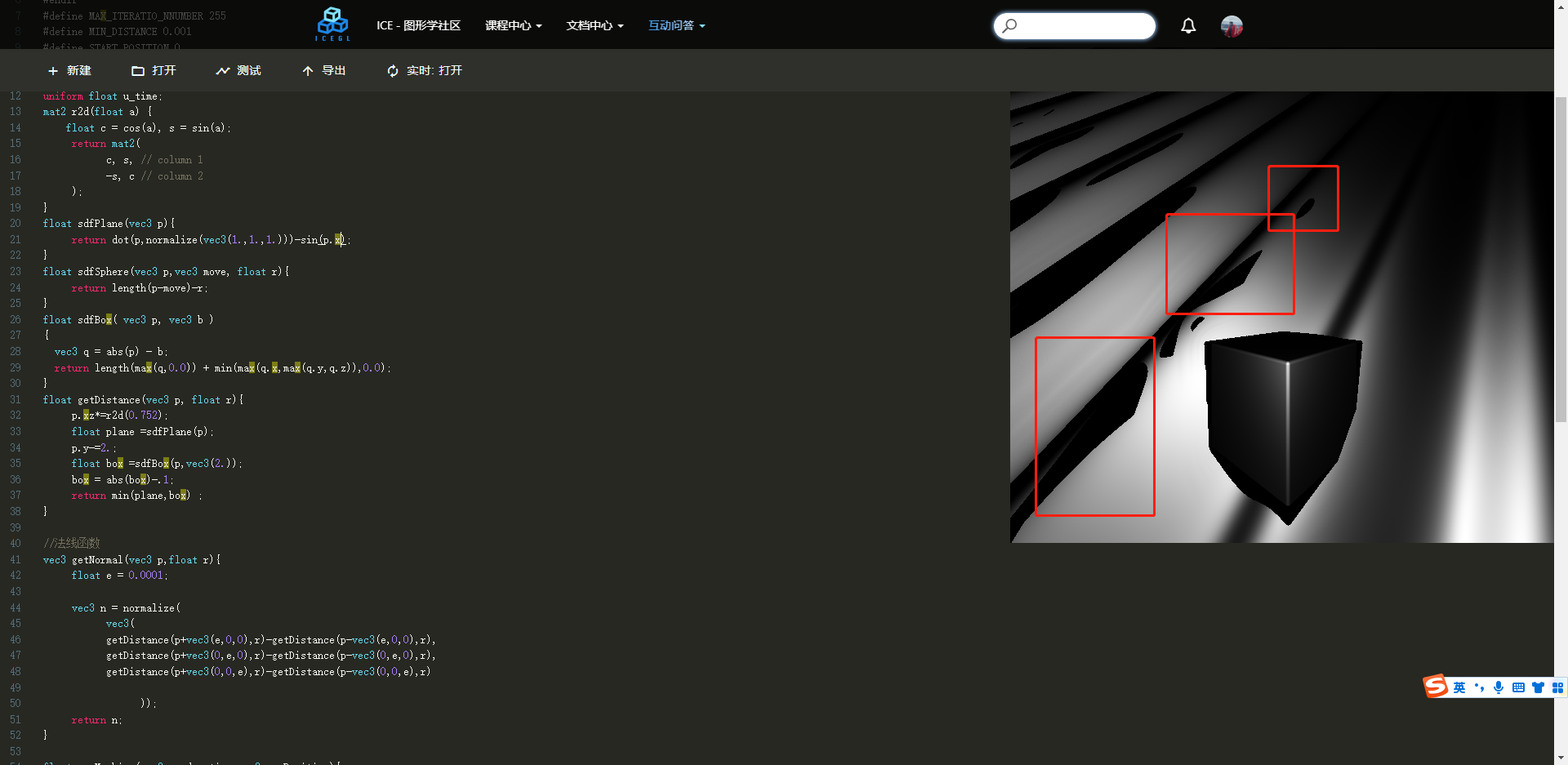
float sdfPlane(vec3 p){
    return dot(p,normalize(vec3(0.,1.,0.)))-sin(p.x);
}
float sdfBox( vec3 p, vec3 b )
{
  vec3 q = abs(p) - b;
  return length(max(q,0.0)) + min(max(q.x,max(q.y,q.z)),0.0)-sin(p.x*5.5+u_time*0.5)*0.2;
}

但是我们发现这样并不是完美的，可以看下图：
不完美.png

冰哥说：如何解决这个问题呢？造成这个问题的原因其实也很简单，就是我们的光线追踪 vec3 p =eyePosition+ d* eyedrection;，随着d距离的不断累加，sin(p.x)几何体本身变得越加瘦小，如果你如果让sin函数振幅更大变成sin(p.x*2.5),其几何体会更加瘦小，射线与几何体的表面相交的点不在原有几何体的表面。故造成此原因。ok，我们采用的方法是利用abs函数回退射线的位置，请看下面代码：

float rayMaching(vec3 eyedrection,vec3 eyePosition){
    float d = START_POSITION;
    
    for(int i = 0;i<MAX_ITERATIO_NNUMBER;i++){
        vec3 p =eyePosition+ d* eyedrection;
      
        float newd  = getDistance(p ,2.);
        d+=newd;
        if(abs(newd)<MIN_DISTANCE||d>END_POSITION){
            break;
        }
    }
     return d ;
}

冰哥说：有的小伙伴问为什么应用abs函数就会使得光线追踪后退呢，其实和我们后面会讲，abs实际是让进入几何体内部的光线追踪，求反。回到与里面点对称的外面的位置，请看图

sin函数波浪原理.png

sin函数波浪问题原理.png

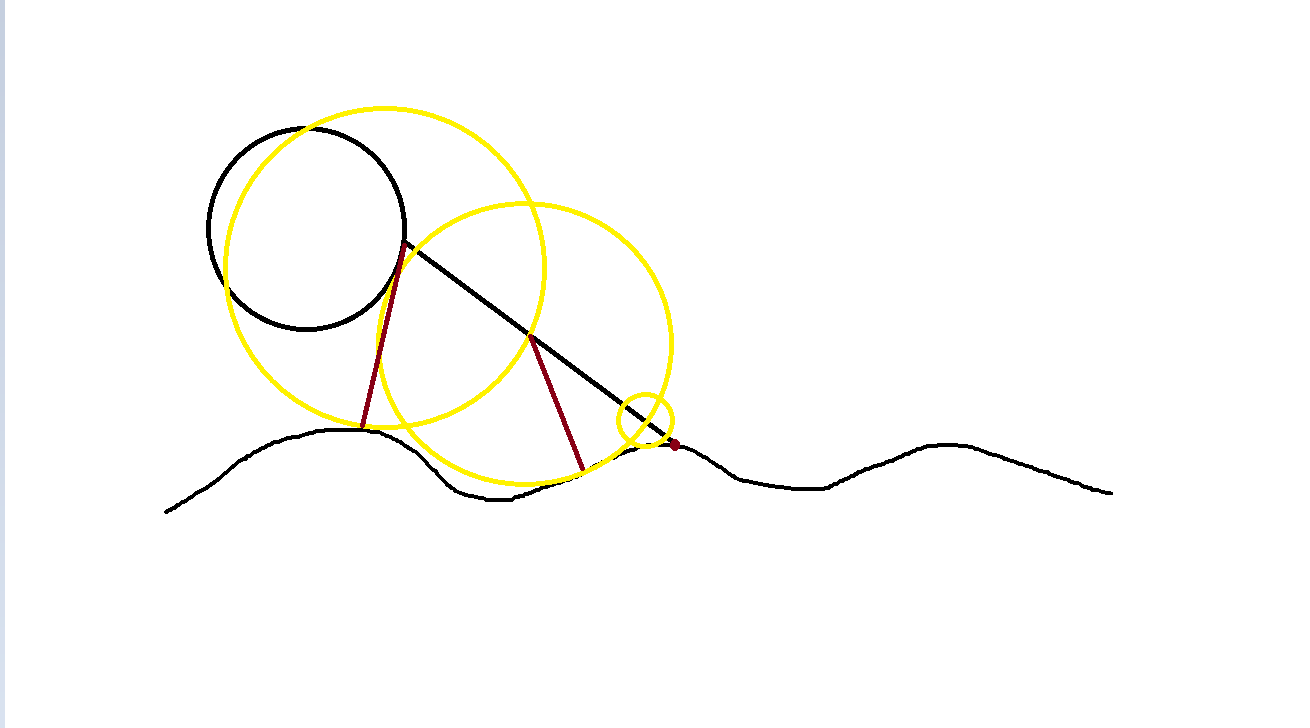
除了上述应用abs函数的方法，我们还有一种方法解决这个问题，就是是我们光线行进的步长变慢一些，但这往往会更加消耗gpu的计算量，不建议经常使用。如下列函数，我们在整getDistance函数返回值上乘一个比例系数，使得行进步数变慢。

float getDistance(vec3 p, float r){
    p.xz*=r2d(0.752);
    float plane =sdfPlane(p);
    p.y-=2.;
    float box =sdfBox(p,vec3(2.));
    box = abs(box)-.1;
    return min(plane,box)*0.3 ;
}
// Author: ice
// Title: 光线追踪

#ifdef GL_ES
precision mediump float;
#endif
#define MAX_ITERATIO_NNUMBER 255
#define MIN_DISTANCE 0.001
#define START_POSITION 0.
#define END_POSITION 100.
uniform vec2 u_resolution;
uniform float u_time;
mat2 r2d(float a) {
    float c = cos(a), s = sin(a);
    return mat2(
        c, s, // column 1
        -s, c // column 2
    );
}
float sdfPlane(vec3 p){
    return dot(p,normalize(vec3(0.,1.,0.)))+sin(p.x*1.5);
}
float sdfSphere(vec3 p,vec3 move, float r){
    return length(p-move)-r;
}
float sdfBox( vec3 p, vec3 b )
{
  vec3 q = abs(p) - b;
  return length(max(q,0.0)) + min(max(q.x,max(q.y,q.z)),0.0)-sin(p.x*5.5+u_time*0.5)*0.2;
}
float getDistance(vec3 p, float r){
  
    float plane =sdfPlane(p);
    p.y-=2.;
    float box =sdfBox(p,vec3(5.,2.,1.));

    return min(plane,box) ;
}

//法线函数
vec3 getNormal(vec3 p,float r){
    float e = 0.0001;
    
    vec3 n = normalize(
        vec3(
        getDistance(p+vec3(e,0,0),r)-getDistance(p-vec3(e,0,0),r),
        getDistance(p+vec3(0,e,0),r)-getDistance(p-vec3(0,e,0),r),
        getDistance(p+vec3(0,0,e),r)-getDistance(p-vec3(0,0,e),r)
            
            ));
    return n;
}

float rayMaching(vec3 eyedrection,vec3 eyePosition){
    float d = START_POSITION;
    
    for(int i = 0;i<MAX_ITERATIO_NNUMBER;i++){
        vec3 p =eyePosition+ d* eyedrection;
      
        float newd  = getDistance(p ,2.);
        d+=newd;
        if(abs(newd)<MIN_DISTANCE||d>END_POSITION){
            break;
        }
    }
     return d ;
}


void main() {
    vec2 uv = (gl_FragCoord.xy*2.-u_resolution.xy)/min(u_resolution.x,u_resolution.y);
    vec3 col = vec3(0.);
    vec3 eyeposition  = vec3(0, 6,10.);
    vec3 eyedrection  =normalize( vec3(uv,-1.));
    float d = rayMaching(eyedrection,eyeposition);
    

    //光线检测后的坐标p
    vec3  p = eyeposition+eyedrection*d;
    vec3 lightPosition = vec3(0, 5, 6);
    //围绕着xz轴旋转
    lightPosition.xz *=r2d(u_time*0.) ;
    vec3 lightDirection = normalize(lightPosition-p);
    vec3 n = getNormal(p,2.);
    float diff =clamp(dot(n, lightDirection), 0., 1.);
    
    //创造阴影
    float shdowd = rayMaching(lightDirection,p+n*0.01);
    if(shdowd<length(lightPosition-p)){diff *= 0.1;} 
    col = vec3(diff );
    col = pow(col, vec3(3.));    
    gl_FragColor = vec4(col,1.0);
}

绘制“麻花”

“麻花”是我自己起的一个名词，其实关键的在于模型自身随着高度增加的螺旋变化。所谓螺旋变化必然涉及到，放大缩小功能还有旋转操作，我们分步骤来看。

首先，模型放大与缩小。smoothstep函数在中级教学给大家讲过，p.y小于0的时候返回0，大于1的时候返回1。再者结合mix函数，smoothstep返回0的时候，mix最终结果就是1.5，返回1的时候最终结果就是4。

    float scale = mix(1.5,4.,smoothstep(0.,1.,p.y));
    p.xz *=scale;

之后，我们再让p.xz乘上放大/缩小系数就可以实现模型随着p.y的大小，变大或者缩小。总的函数代码如下所示

float getDistance(vec3 p, float r){
  
    float plane =sdfPlane(p);
    p.y-=5.0;
 
    float scale = mix(1.5,4.,smoothstep(0.,1.,p.y));
    p.xz *=scale;
    float box =sdfBox(p,vec3(2.));
    return min(plane,box)/scale/10. ;
}

之后，实现随高度旋转。这里面核心还是旋转矩阵。这块我们前面讲过多次，不再赘述。

mat2 r2d(float a) {
    float c = cos(a), s = sin(a);
    return mat2(
        c, s, // column 1
        -s, c // column 2
    );
}

下面代码是将旋转与高度p.y相互关联，实现随着高度变化，实现旋转变化。

   mat2 roation = r2d(smoothstep(0.,2.,p.y));
   p.xz *=roation;
// Author: ice
// Title: 光线追踪

#ifdef GL_ES
precision mediump float;
#endif
#define MAX_ITERATIO_NNUMBER 255
#define MIN_DISTANCE 0.001
#define START_POSITION 0.
#define END_POSITION 100.
uniform vec2 u_resolution;
uniform float u_time;
mat2 r2d(float a) {
    float c = cos(a), s = sin(a);
    return mat2(
        c, s, // column 1
        -s, c // column 2
    );
}
float sdfPlane(vec3 p){
    return dot(p,normalize(vec3(0.,1.,0.)));
}
float sdfSphere(vec3 p,vec3 move, float r){
    return length(p-move)-r;
}
float sdfBox( vec3 p, vec3 b )
{
  vec3 q = abs(p) - b;
  return length(max(q,0.0)) + min(max(q.x,max(q.y,q.z)),0.0);
}
float getDistance(vec3 p, float r){
  
    float plane =sdfPlane(p);
    p.y-=5.;
    
    // p.x = abs(p.x);
    //  p.x -=4.;
    vec3 n =   normalize(vec3(0.,1.,0.));
    p-=2.*n*min(0.,dot(p,n));
    float scale = mix(1.5,4.,smoothstep(0.,1.,p.y));
    p.xz *=scale;
    mat2 roation = r2d(smoothstep(0.,2.,p.y));
    p.xz *=roation;
   
    float box =sdfBox(p,vec3(2.));

    return min(plane,box)/scale/10. ;
}

//法线函数
vec3 getNormal(vec3 p,float r){
    float e = 0.0001;
    
    vec3 n = normalize(
        vec3(
        getDistance(p+vec3(e,0,0),r)-getDistance(p-vec3(e,0,0),r),
        getDistance(p+vec3(0,e,0),r)-getDistance(p-vec3(0,e,0),r),
        getDistance(p+vec3(0,0,e),r)-getDistance(p-vec3(0,0,e),r)
            
            ));
    return n;
}

float rayMaching(vec3 eyedrection,vec3 eyePosition){
    float d = START_POSITION;
    
    for(int i = 0;i<MAX_ITERATIO_NNUMBER;i++){
        vec3 p =eyePosition+ d* eyedrection;
      
        float newd  = getDistance(p ,2.);
        d+=newd;
        if(abs(newd)<MIN_DISTANCE||d>END_POSITION){
            break;
        }
    }
     return d ;
}


void main() {
    vec2 uv = (gl_FragCoord.xy*2.-u_resolution.xy)/min(u_resolution.x,u_resolution.y);
    vec3 col = vec3(0.);
    vec3 eyeposition  = vec3(0, 6,10.);
    vec3 eyedrection  =normalize( vec3(uv,-1.));
    float d = rayMaching(eyedrection,eyeposition);
    

    //光线检测后的坐标p
    vec3  p = eyeposition+eyedrection*d;
    vec3 lightPosition = vec3(0, 5, 6);
    //围绕着xz轴旋转
    lightPosition.xz *=r2d(u_time*0.) ;
    vec3 lightDirection = normalize(lightPosition-p);
    vec3 n = getNormal(p,2.);
    float diff =clamp(dot(n, lightDirection), 0., 1.);
    
    //创造阴影
    float shdowd = rayMaching(lightDirection,p+n*0.01);
    if(shdowd<length(lightPosition-p)){diff *= 0.1;} 
    col = vec3(diff );
    col = pow(col, vec3(3.));    
    gl_FragColor = vec4(col,1.0);
}

参考文献

推荐IQ的博客过于三维SDF，后续我们继续讲解其他的sdf生成规则。

https://iquilezles.org/articles/distfunctions/min函数.png

1人点赞 发表评论 分享 收藏 感谢 举报
0 条评论
暂无评论，快来发表评论吧
请登录后再发布评论，点击登录
登录 注册新账号

相关文章

1
shader绘制二维爱心

热门文章

1
WebGL通常的错误提示以及解决方法
2
几何学——矩阵基础知识汇总
3
几何学——欧拉角与万向锁看这一篇就够了(含threejs demo演示)
4
几何学——坐标系概括
5
初步探讨一下Shader中的SDF应用
6
超详细讲解UE5材质基础
7
几何学——矢量的几何运算
8
shader通常的错误提示以及解决方法
9
npm 及 yarn 代理设置及更换为国内下载源
10
几何学——点、向量和法线

热门问题

1
UE5中，新建关卡为什么是漆黑一片？如何设置？
2
Cesium展示3D格点数据（原始数据为nc格点数据）进行体绘制渲染思路
3
煤矿三维数字点云项目需求
4
webgl怎么添加git动图呢
5
最近想学习webgl，不知道从哪里入手，请问有什么具体学习路线嘛？
6
threejs怎么生成antv或者deckgl具有聚合效果的热力图
7
Threejs/webgl高级人才招聘
8
cesium绘制路线,然后模型根据路线运动动画
9
视口设置有区别导致帧缓冲的纹理渲染不出来
10
请教一下关于cesium的GIS方面的问题，街道数据的获得

热门标签

shader WebGL cesium threeJS gis vue3 招聘 glsl 地图数据 vite TvT 城市gis VUE 模型 绘制点 UE5 自定义着色器 vue3-ts-cesium-map-show cesium贴图材质 点击事件 useTresContext @tresjs/core 实现热力图 求助 三维图表 html css webGPU 学习线路 GeoJson dwg模型加载 初级课程鼠标绘点 drawElements纹理 图形学基础 图层 建模 blender 几何 vscode vec3 fastadmin导入插件 three MacOS 升级Cesium版本 着色器 _model._sourcePrograms为空 3D格点数据 算法 mapv glmatrix

等待解答

问
深圳知名运动相机招聘。
问
硅谷base初创招聘软件工程师
问
TvT或Threejs中报错，Uncaught TypeError: ‘get‘ on proxy: property ‘modelViewMatrix‘ is a read-only and non
问
基于mapbox的风场交互问题
问
Java与Android武汉腾讯招聘要求
问
使用cesium实现对折线的每个点的编辑，按住x,y,z可向三个方向拖动
问
诚聘WebGIS工程师
问
webgl+建模讲师招聘
问
煤矿三维数字点云项目需求
问
Threejs/webgl高级人才招聘

推荐达人

发呆的石头
发呆的石头
3个答案 0次被采纳
JesueLike
JesueLike
3个答案 0次被采纳
何贤
何贤
0个答案 0次被采纳
七个隆咚锵
七个隆咚锵
2个答案 0次被采纳
sunny
sunny
2个答案 2次被采纳

发布
问题