几何学——插值函数概括

背景

插值是计算机图形学中非常常用的技术。数据通常指定在规则网格上（已知 1D、2D 或 3D 网格的顶点位置），需要自动计算出其他随机位置的值。如果样本位于网格顶点，那么我们可以简单地使用存储在那里的值。但是，如果样本位于网格上的其他任何位置（单元格中的某个位置），那么考虑到我们在那里没有数据，我们需要通过对存储在单元格顶点的值求平均值来计算一个。这种技术称为插值。

在 2D 中，该技术称为双线性插值。在 3D ，称为三线性插值。线性插值是这样一种方程：

$$ a(1-t)+bt \quad with \quad 0 \le t \le 1 $$

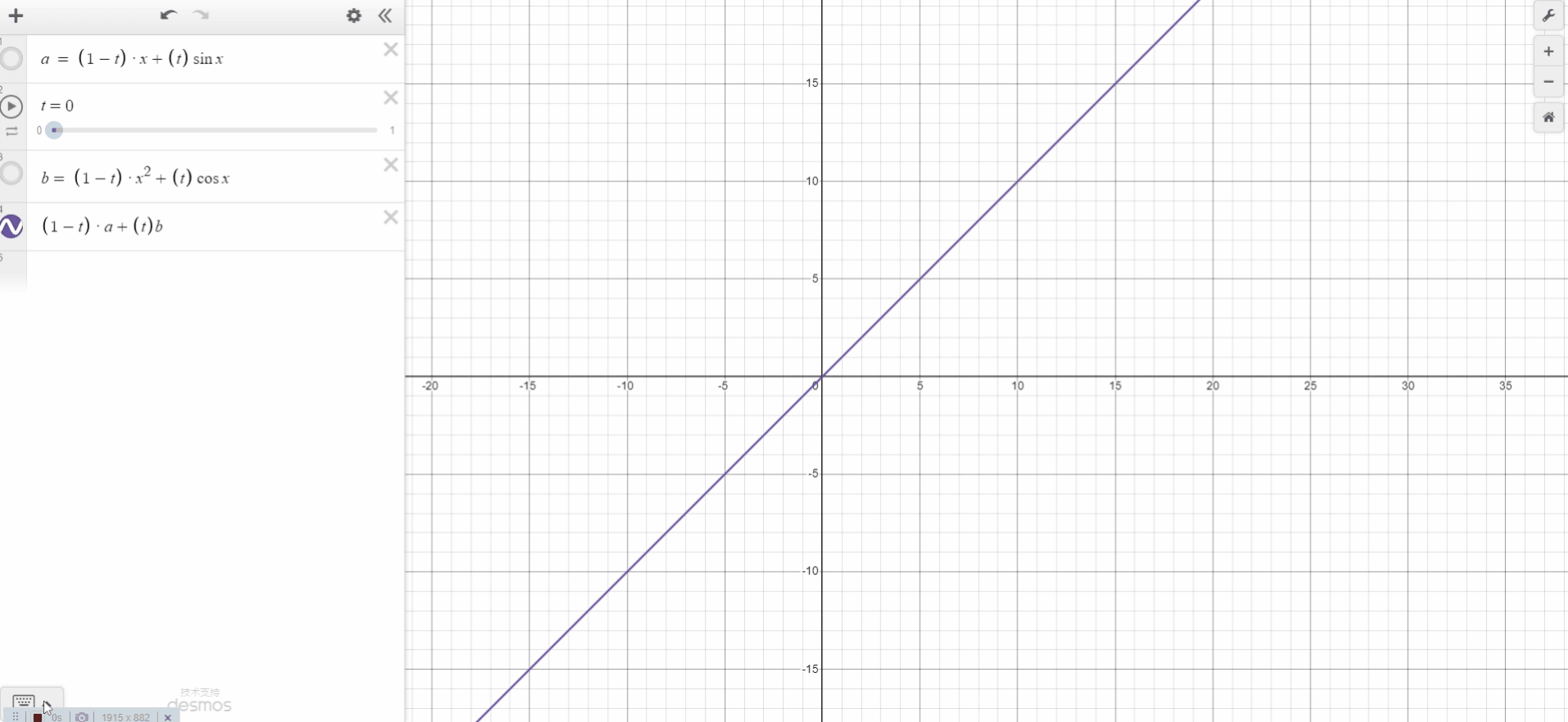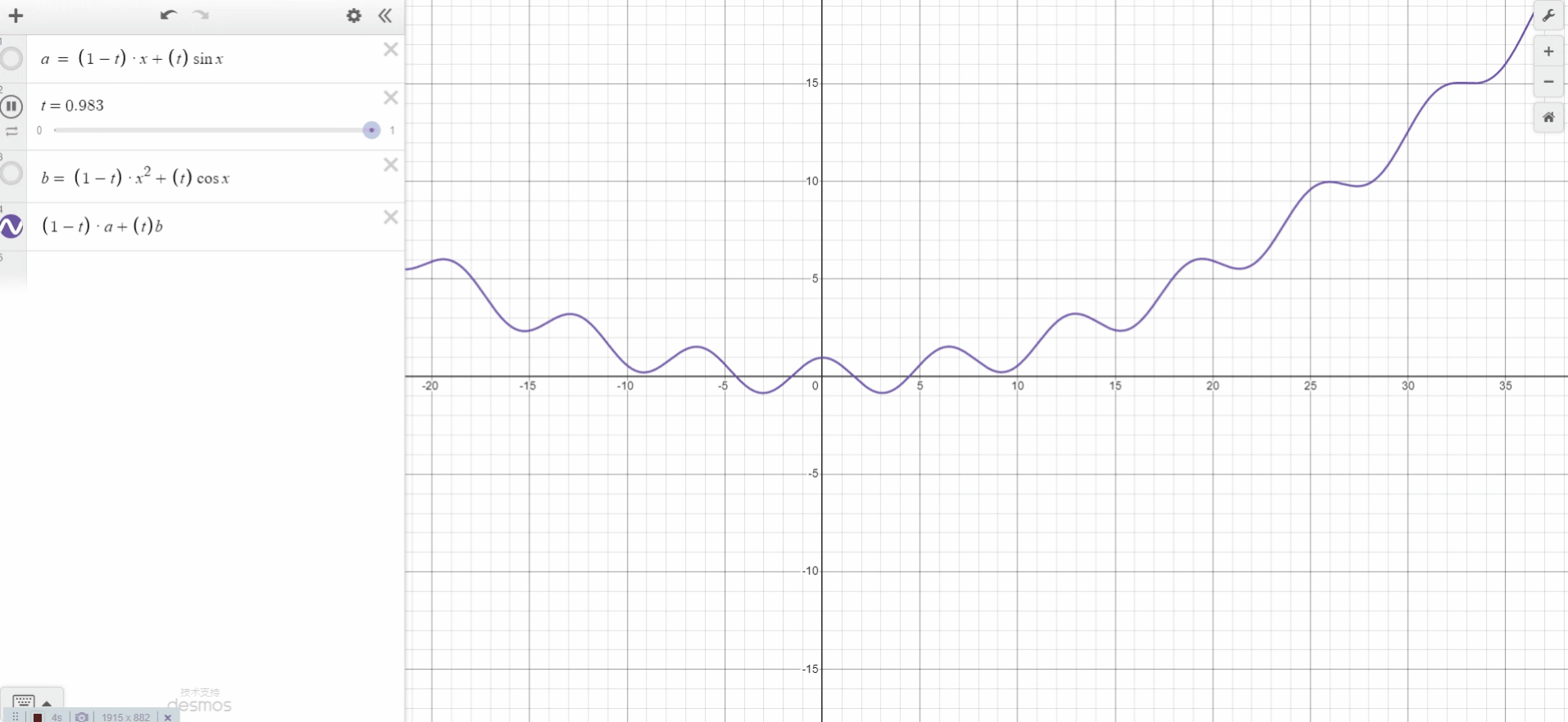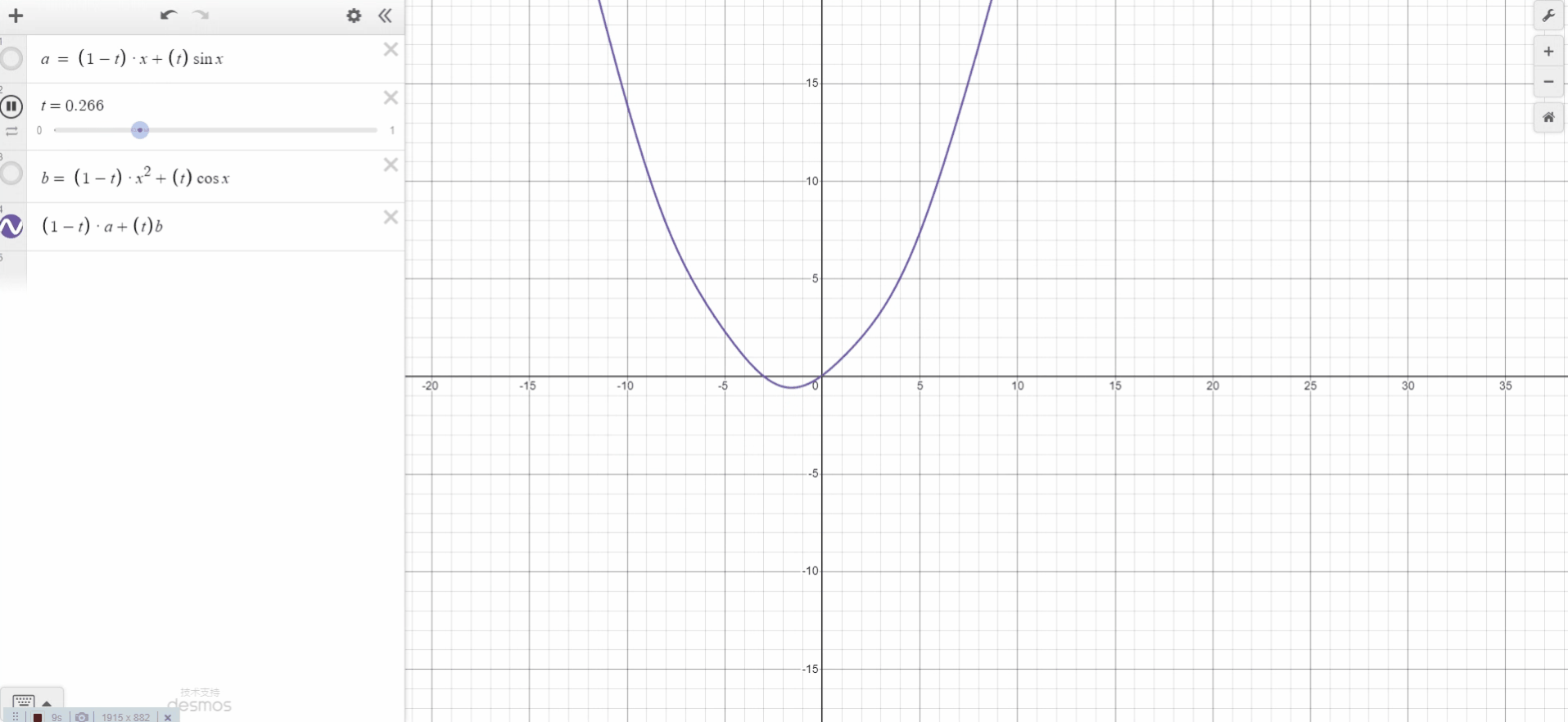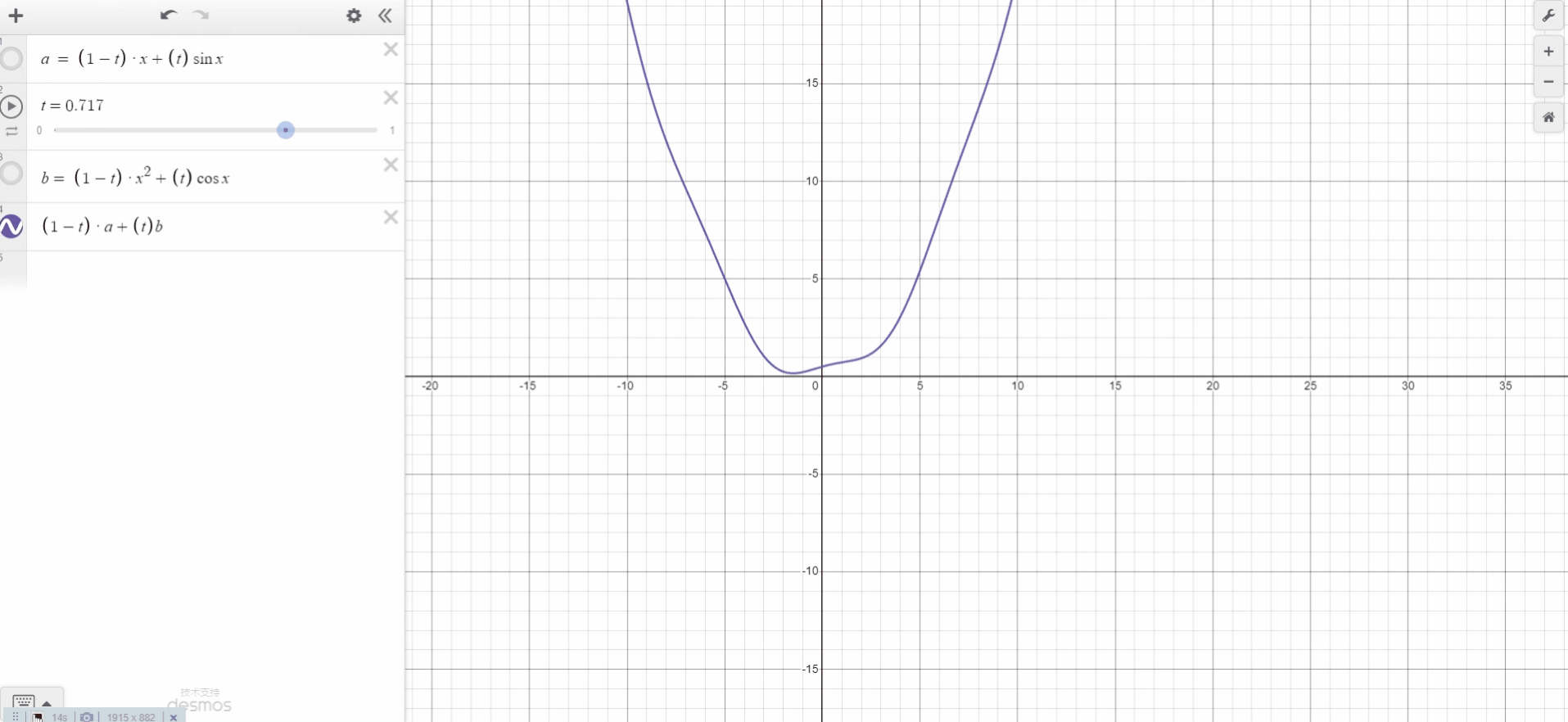
这种方法很简单，只需要两个值（a 和 b）和一些简单的算术运算。请注意，t 在 0 到 1的范围内。基于线性插值，我们desmos模拟出了线性插值实例。

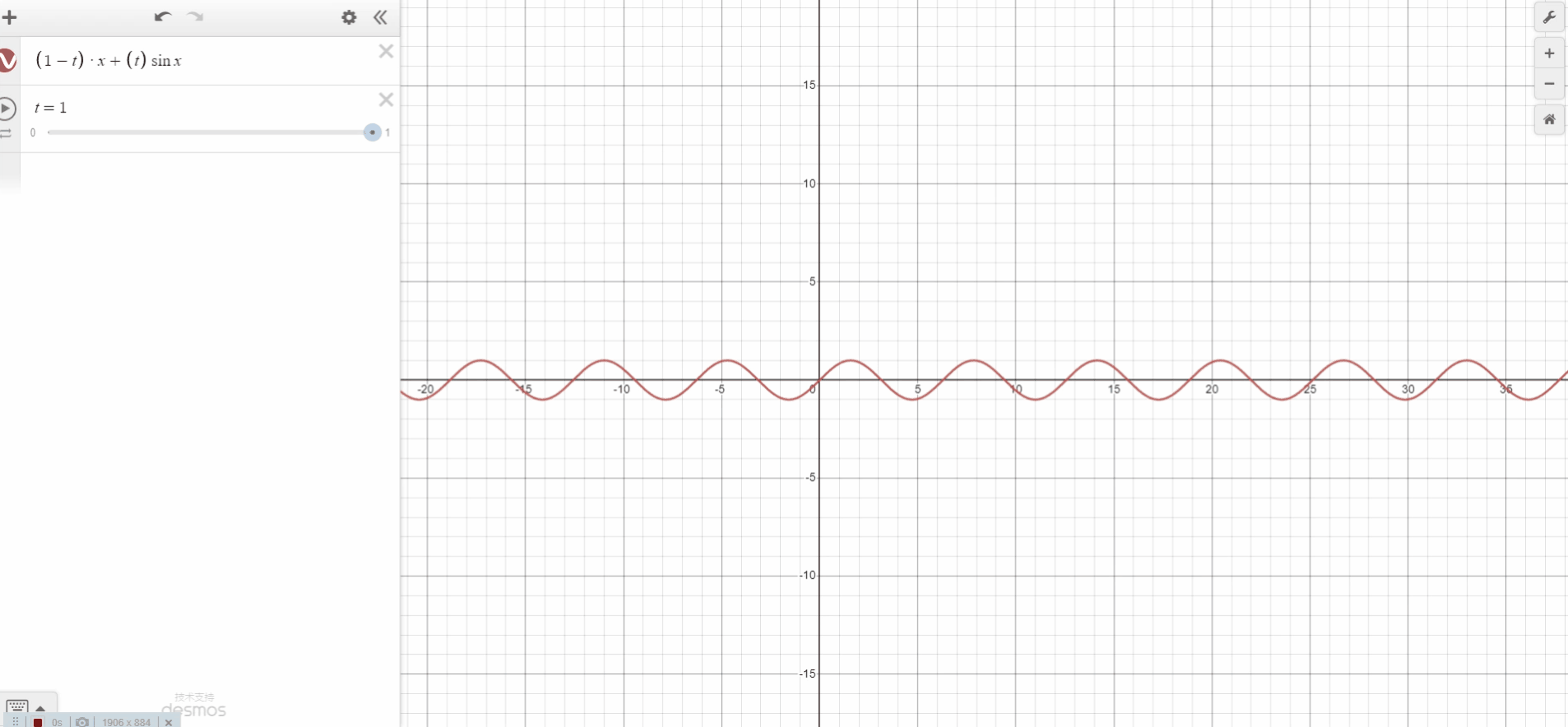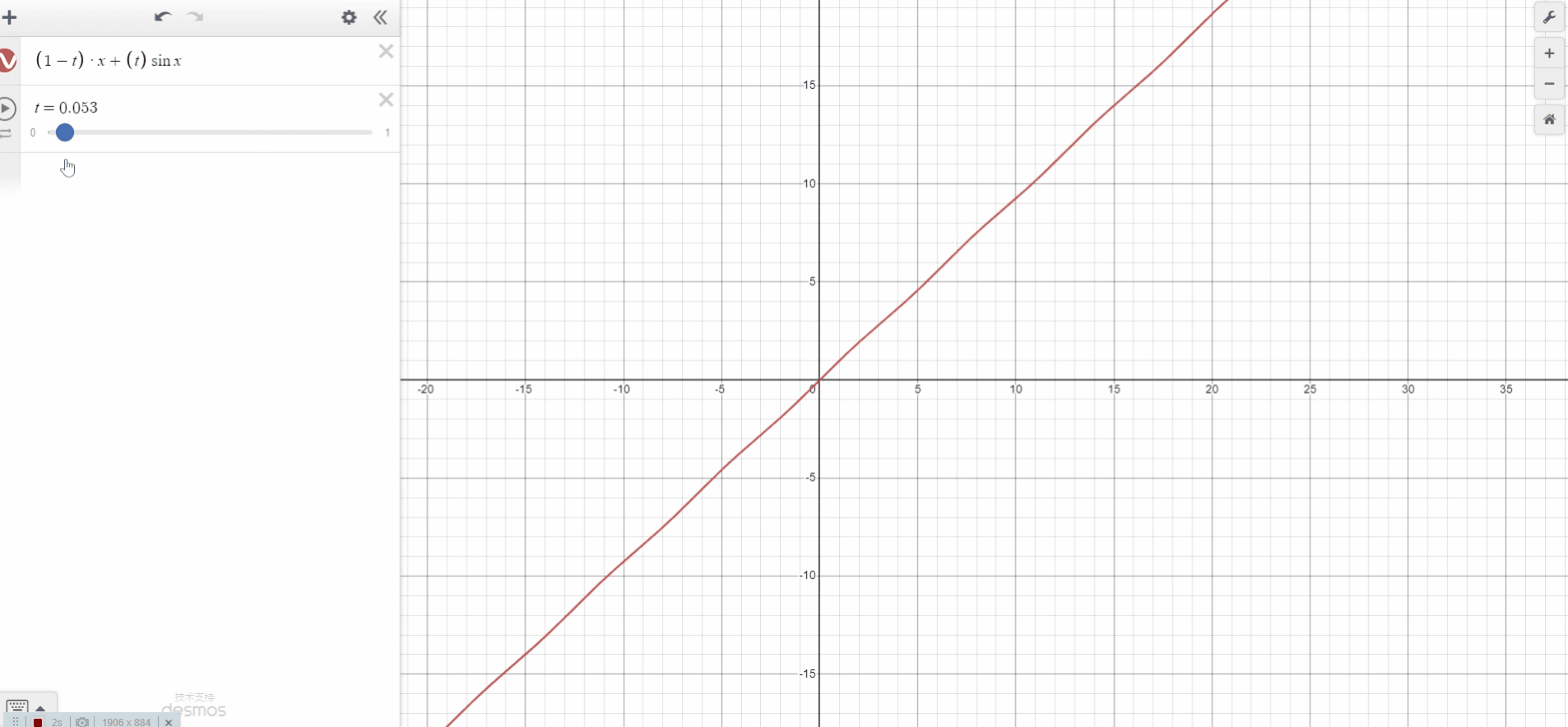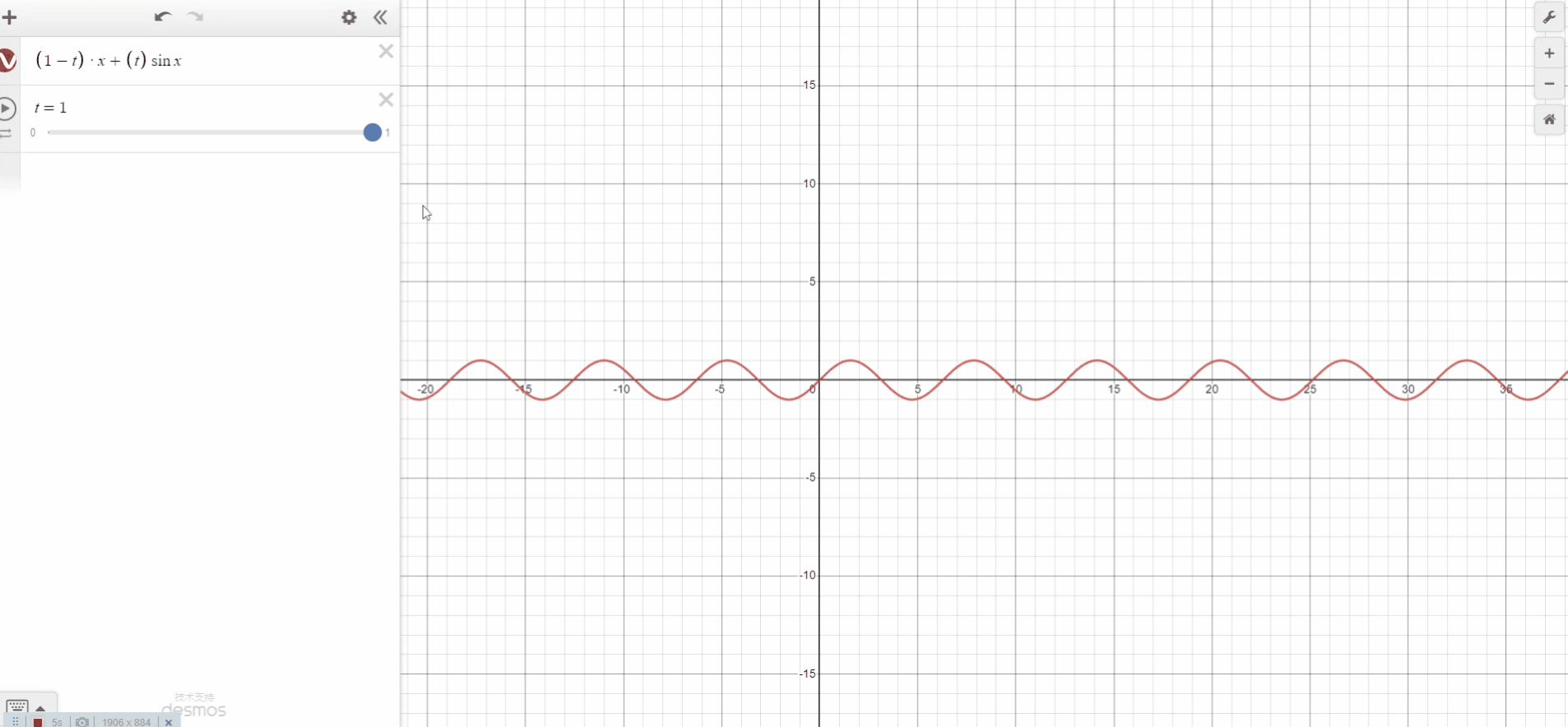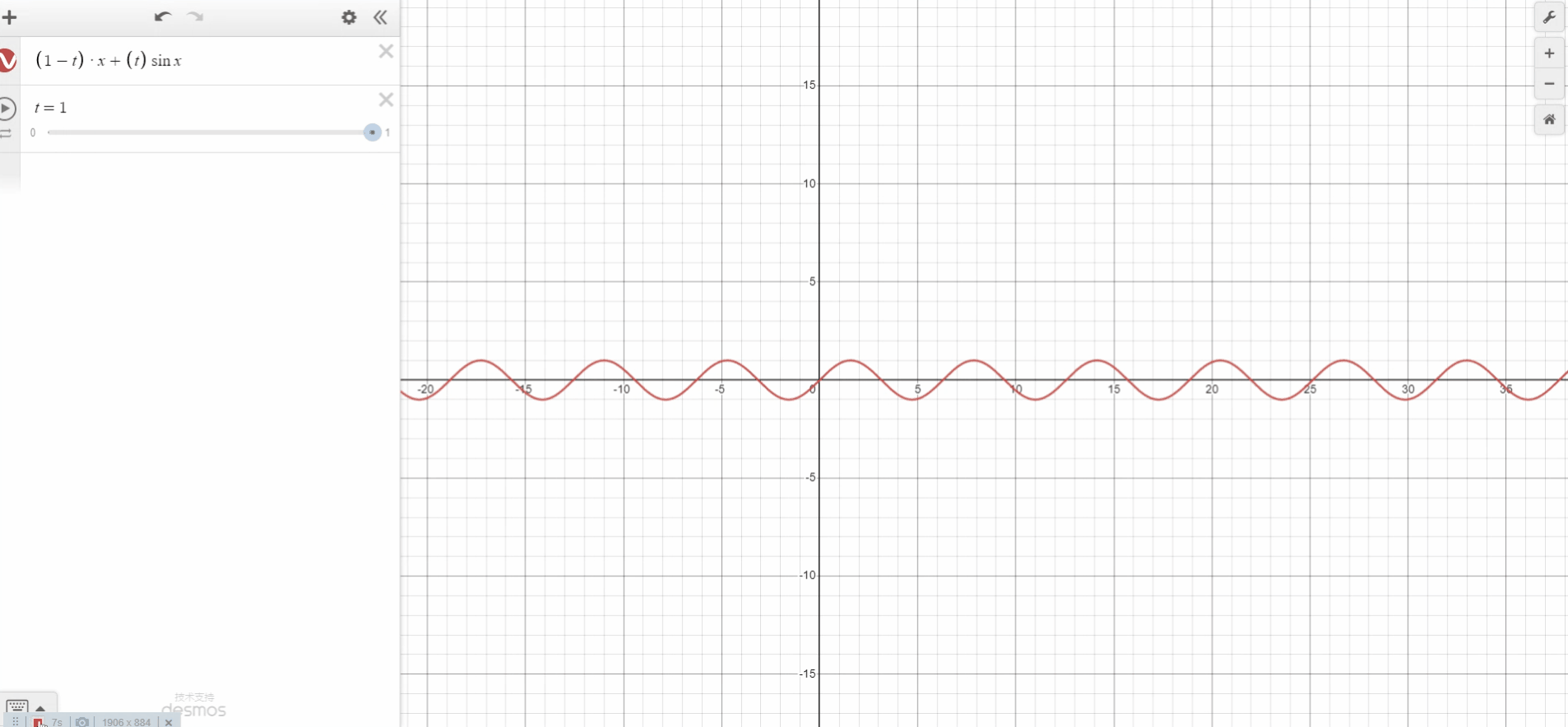
插值技术常用于图像处理（例如调整图像大小）。但是 3D 技术也可以利用 3D 或 2D 网格（纹理可以看作是 2D 网格），例如流体模拟、体积渲染、纹理映射和辐照度缓存等等。

双线性插值

双线性插值是基于1维线性插值的拓展，双线性插值。如下图所示。

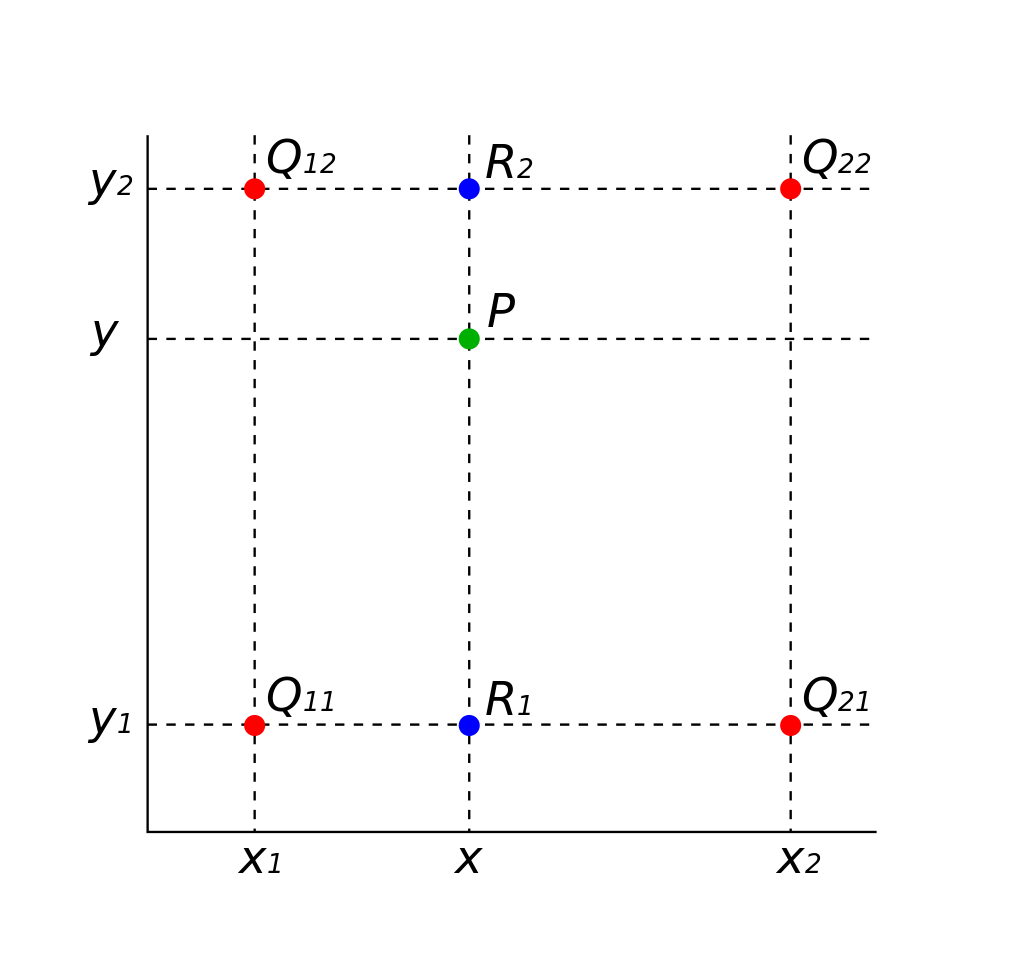
基于双线性插值，我们desmos模拟出了双线性插值实例。

如图所示，我们需要求P点的像素值。我们已知了Q11、Q21、Q12、Q22、P的坐标。也知道Q11、Q21、Q12、Q22的像素值。所以先用关于X的单线性插值去分别计算R1、R2的像素值

$$ \begin{gathered} f(x,y_1) \approx\dfrac{x_2-x}{x_2-x_1}f(Q_{11}) + \dfrac{x-x_1}{x_2-x_1}f(Q_{12}), \\ f(x,y_2) \approx\dfrac{x_2-x}{x_2-x_1}f(Q_{12})+\dfrac{x-x_1}{x_2-x_1}f(Q_{22}). \end{gathered} $$

在右边的等式中的字母f(Q11)、f(Q12)、f(Q21)、f(Q22)、x1、x2、x都是已知的，求出的f(x,y1)与f(x,y2）即为R1、R2的像素值。再使用关于y方向的单线性插值计算P点的像素值得出：

$$ f(x,y)\approx\frac{y_2-y}{y_2-y_1}f(x,y_1)+\frac{y-y_1}{y_2-y_1}f(x,y_2) $$

在右边的等式中的字母y1、y2、y都是已知的，f(x,y1)与f(x,y2）即为上一个式子中求出的R1、R2像素值。以下是一维线性插值和二维线性插值的几何区别。

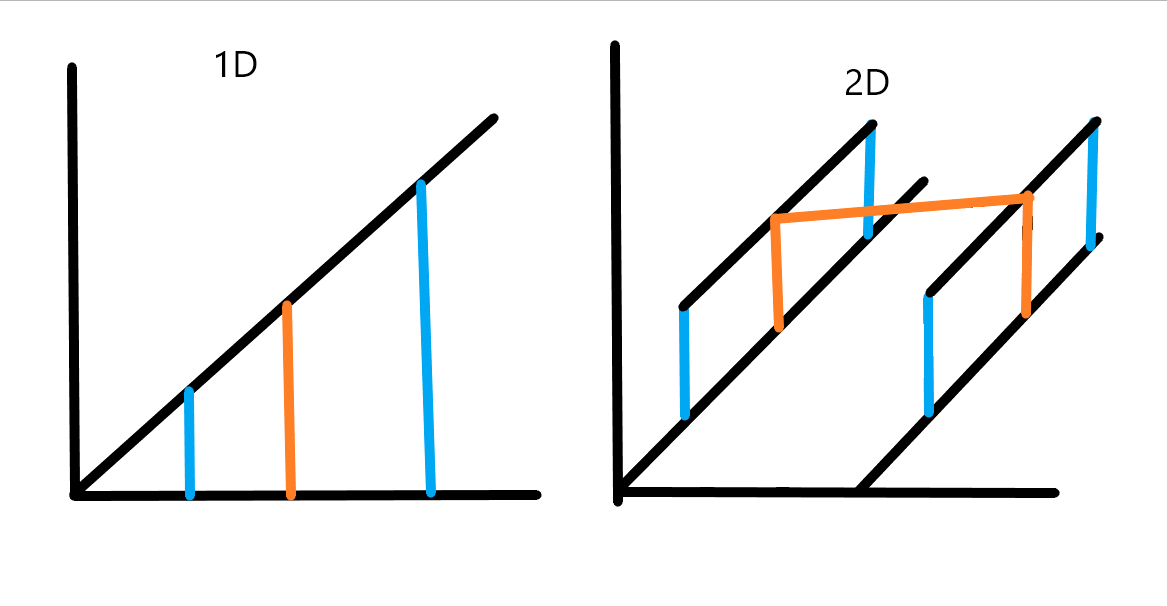
冰哥说：有的小伙伴可能对于f(Q11)、f(Q12)、f(Q21)、f(Q22)比较疑惑，实际上它们代表的是任何想要插值的内容，可以是颜色，也可以是数字。总是它代表着的是被插值的四个端点值。另外（x2-x）/（x2-x1）和（x-x1）/（x2-x1）的值范围都是[0,1]之间。实际上我们在shader中给大家介绍的mix函数就是采用的类插值的方法。

三线性插值

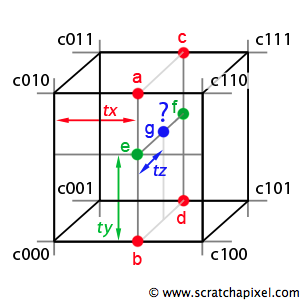
三线性是双线性插值技术的直接扩展。它可以看作是两个双线性插值（一个用于单元正面，一个用于背面）的线性插值。为了计算 e 和 f，我们使用上一章中描述的技术使用两个双线性插值。为了计算 g，我们沿 z 轴对 e 和 f 进行线性插值（使用 tz，它是样本点 g 的 z 坐标）。

我们执行四个线性插值以使用 tx 计算 a、b、c 和 d，然后我们通过使用 ty 对 a、b、c 和 d 进行插值来计算 e 和 f，最后我们通过使用 tz 对 e 和 f 进行插值来找到我们的样本点。

三线性插值与其二维插值具有相同的优点和缺点。它快速且易于实施，但不会产生非常流畅的结果。但是，对于体积渲染或流体模拟等需要在 3D 网格中进行大量查找的情况，它仍然是一个非常好的选择。

总结

线性插值的用法挺广泛的，接触最多就是在shader中，用于在两个顶点之间进行插值以创建平滑的过渡效果。举个类似的例子：

vec3 lerp(vec3 start, vec3 end, float percent) {
  return (1.0 - percent) * start + percent * end;
}

该函数接受三个参数：起始点 start，结束点 end 和一个百分比 percent。它返回起始点和结束点之间按比例插值后的结果。为了达到类似效果shader中还给我们提供mix函数，比如以下代码：

vColor = mix(color, vec3(1.0, 0.0, 0.0),t);

后面我们在实战或者在视频课程中再给大家详细讲解有关例子。

参考文献

https://blog.csdn.net/eurus_/article/details/102755898

https://en.wikipedia.org/wiki/Trilinear_interpolation