在 3D 编程的世界中，有时数学知识非常重要。我们前面给大家讲过矩阵，矩阵能做很事情，但是矩阵同样具有着很多局限性，四元数实际上为了解决矩阵在某些方面的问题，而诞生的一种全新的数学表达式。接下来我们详细介绍下四元数。

概念

四元数是数学中的概念之一。四元数用于 3D 编程中涉及旋转的许多操作。举个例子：

当在三维空间中放置某种模型时，模型的姿势我怎么能表示呢？不是模型的坐标位置。这里的姿势是指模型如何倾斜，或者模型朝向什么方向。当然你可以用矩阵表示，但是矩阵并不是一个专门用来表示姿态的公式，它更加的复杂，所有我们迫切的需要一种表达方式来表达模型在空间中的位置信息。看看下面这张图。

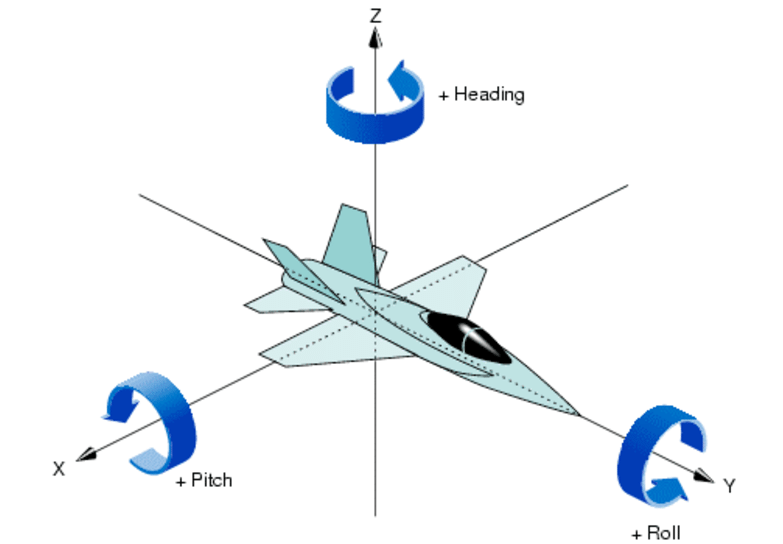
为了表示姿势，最少的信息是[它旋转了多少] 和 [轴的哪个方向] 这是必须的。所有的姿势都可以只用这两个元素来表达。

所以四元数它到底是什么？

四元数可用于表示关于任意方向的任意角度的旋转。这是一个四元数就可以表达出各种姿势这就是它的意思。

记法

一个四元数包含一个标量分量和一个3D 向量分量。经常记标量分量为 w，记向量分量为单一的v或分开的x，y，z。两种记法分别如下:

[w,v]
[w,(x,y,z)]

假设n 为转轴。对于转轴来说长度并不重要，将n 定义为单位长度会比较方便。根据左手或右手法则，n 的方向定义了哪边将被认为是旋转“正”方向,θ设为绕轴旋转的量。因此，(n,θ)定义了绕n指定的轴旋转θ角。但是往往四元数没有这么简单的表示。

$$ \begin{aligned} & \mathbf{1}=\left[\cos(\theta/2)\quad\sin(\theta/2)\mathbf{n}\right] \\ &=\left[\cos(\theta/2)\quad(\sin(\theta/2)\mathbf{n}_{x}\quad\sin(\theta/2)\mathbf{n}_{y},\quad\sin(\theta/2)\mathbf{n}_{z})\right] \end{aligned} $$

运算

叉乘

直接甩公式吧，有兴趣的可以自行推解一下，因为我们后面主要是应用四元数，所以对于公式的由来不是那么重要：

$$ \begin{bmatrix}w_{1},(x_{1},y_{1},z_{1})\end{bmatrix}]\begin{bmatrix}w_{2},(x_{2},y_{2},z_{2})\end{bmatrix}=\begin{gathered} \left[\begin{array}{c}{w_{1}w_{2}-x_{1}x_{2}-y_{1}y_{2}-z_{1}z_{2}}\\ {w_{1}x_{2}+x_{1}w_{2}+z_{1}y_{2}-y_{1}z_{2}}\\ {w_{1}y_{2}+y_{1}w_{2}+x_{1}z_{2}-z_{1}x_{2}}\\ \end{array}\right] \\ \left\lfloor{w_{1}z_{2}+z_{1}w_{2}+y_{1}x_{2}-x_{1}y_{2}},\right\rfloor \end{gathered} $$

另外一种是简化的：

$$ \begin{bmatrix}w_{1},v_{1}\end{bmatrix}\begin{bmatrix}w_{2},v_{2}\end{bmatrix}=\left[\begin{matrix}{w_{1}w_{2}-\mathbf{v}_{1}\cdot\mathbf{v}_{2}},{\mathbf{w}_{1}\mathbf{v}_{2}+\mathbf{w}_{2}\mathbf{v}_{1}+\mathbf{v}_{2}\mathbf{v}_{1}+\mathbf{v}_{2}\times\mathbf{v}_{1}}\\ \end{matrix}\right]. $$

点乘

$$ \mathbf{q}_{1}\cdot\mathbf{q}_{2}=\left[\begin{matrix}{w}_{1},{\mathbf{v}_{1}}\\ \end{matrix}\right]\cdot\left[\begin{matrix}{w}_{2},{\mathbf{v}_{2}}\\ \end{matrix}\right]=w_{1}\dot{w}_{2}+\mathbf{v}_{1}\cdot\mathbf{v}_{2}=\begin{bmatrix}w_{1},(x_{1},y_{1},z_{1})\end{bmatrix}]\begin{bmatrix}w_{2},(x_{2},y_{2},z_{2})\end{bmatrix}=w_{1}w_{2}+x_{1}x_{2}+y_{1}y_{2}+z_{1}z_{2} $$

四元数点乘的几何解释类似于向量点乘的几何解释。四元数点乘a·b 的绝对值越大，a和b代表的角位移越“相似”。

"差"

如果我们要求的两个四元数中间的“差”值应该如何表示呢？

利用四元数的乘法和逆，就能够计算两个四元数的“差”。“差”被定义为一个方位到另一个方位的角位移。换句话说，给定方位 a 和b，能够计算从 a 旋转到 的位d用四元数等式更加紧凑地表示为:
ad=b
(这里使用我们的更加直观的四元数乘法定义，旋转的顺序对应于从左向右乘法的顺序。)现在来求d如果等式中的变量为标量，那么就可以简单的除以 a。但是，不能除以四元数，只能乘它们。也许乘以它的逆能达到想要的效果!两边同时 a必须注意，四元数法不满交换律)

$$ \mathbf{a}^{-1}(\mathbf{a}\mathbf{d})=\mathbf{a}^{-1}\mathbf{b} $$

$$ \begin{gathered} a^{-1}\left(a d\right)=a^{-1}\mathbf{b} \\ \left[\begin{array}{c c}{1}&{\mathbf{0}}\\ \end{array}\right]\mathbf{d}=\mathbf{a}^{-1}\mathbf{b} \\ \mathbf{d}=\mathbf{a}^{-1}\mathbf{b} \end{gathered} $$

现在，我们就有了求得代表一个方位到另一个方位角位移的四元数的方法。两个四元数之间的角度“差”更类似于“除”，而不是真正的“差”(减法)。

小结

最后给大家推荐一个四元数的库，用于大家自主学习，下一期我们给大家做一些四元数的例子，让大家切实将四元数用起来。

// ------------------------------------------------------------------------------------------------
// minMatrixb.js
// version 0.0.2
// Copyright (c) doxas
// ------------------------------------------------------------------------------------------------

function matIV(){
    this.create = function(){
        return new Float32Array(16);
    };
    this.identity = function(dest){
        dest[0]  = 1; dest[1]  = 0; dest[2]  = 0; dest[3]  = 0;
        dest[4]  = 0; dest[5]  = 1; dest[6]  = 0; dest[7]  = 0;
        dest[8]  = 0; dest[9]  = 0; dest[10] = 1; dest[11] = 0;
        dest[12] = 0; dest[13] = 0; dest[14] = 0; dest[15] = 1;
        return dest;
    };
    this.multiply = function(mat1, mat2, dest){
        var a = mat1[0],  b = mat1[1],  c = mat1[2],  d = mat1[3],
            e = mat1[4],  f = mat1[5],  g = mat1[6],  h = mat1[7],
            i = mat1[8],  j = mat1[9],  k = mat1[10], l = mat1[11],
            m = mat1[12], n = mat1[13], o = mat1[14], p = mat1[15],
            A = mat2[0],  B = mat2[1],  C = mat2[2],  D = mat2[3],
            E = mat2[4],  F = mat2[5],  G = mat2[6],  H = mat2[7],
            I = mat2[8],  J = mat2[9],  K = mat2[10], L = mat2[11],
            M = mat2[12], N = mat2[13], O = mat2[14], P = mat2[15];
        dest[0] = A * a + B * e + C * i + D * m;
        dest[1] = A * b + B * f + C * j + D * n;
        dest[2] = A * c + B * g + C * k + D * o;
        dest[3] = A * d + B * h + C * l + D * p;
        dest[4] = E * a + F * e + G * i + H * m;
        dest[5] = E * b + F * f + G * j + H * n;
        dest[6] = E * c + F * g + G * k + H * o;
        dest[7] = E * d + F * h + G * l + H * p;
        dest[8] = I * a + J * e + K * i + L * m;
        dest[9] = I * b + J * f + K * j + L * n;
        dest[10] = I * c + J * g + K * k + L * o;
        dest[11] = I * d + J * h + K * l + L * p;
        dest[12] = M * a + N * e + O * i + P * m;
        dest[13] = M * b + N * f + O * j + P * n;
        dest[14] = M * c + N * g + O * k + P * o;
        dest[15] = M * d + N * h + O * l + P * p;
        return dest;
    };
    this.scale = function(mat, vec, dest){
        dest[0]  = mat[0]  * vec[0];
        dest[1]  = mat[1]  * vec[0];
        dest[2]  = mat[2]  * vec[0];
        dest[3]  = mat[3]  * vec[0];
        dest[4]  = mat[4]  * vec[1];
        dest[5]  = mat[5]  * vec[1];
        dest[6]  = mat[6]  * vec[1];
        dest[7]  = mat[7]  * vec[1];
        dest[8]  = mat[8]  * vec[2];
        dest[9]  = mat[9]  * vec[2];
        dest[10] = mat[10] * vec[2];
        dest[11] = mat[11] * vec[2];
        dest[12] = mat[12];
        dest[13] = mat[13];
        dest[14] = mat[14];
        dest[15] = mat[15];
        return dest;
    };
    this.translate = function(mat, vec, dest){
        dest[0] = mat[0]; dest[1] = mat[1]; dest[2]  = mat[2];  dest[3]  = mat[3];
        dest[4] = mat[4]; dest[5] = mat[5]; dest[6]  = mat[6];  dest[7]  = mat[7];
        dest[8] = mat[8]; dest[9] = mat[9]; dest[10] = mat[10]; dest[11] = mat[11];
        dest[12] = mat[0] * vec[0] + mat[4] * vec[1] + mat[8]  * vec[2] + mat[12];
        dest[13] = mat[1] * vec[0] + mat[5] * vec[1] + mat[9]  * vec[2] + mat[13];
        dest[14] = mat[2] * vec[0] + mat[6] * vec[1] + mat[10] * vec[2] + mat[14];
        dest[15] = mat[3] * vec[0] + mat[7] * vec[1] + mat[11] * vec[2] + mat[15];
        return dest;
    };
    this.rotate = function(mat, angle, axis, dest){
        var sq = Math.sqrt(axis[0] * axis[0] + axis[1] * axis[1] + axis[2] * axis[2]);
        if(!sq){return null;}
        var a = axis[0], b = axis[1], c = axis[2];
        if(sq != 1){sq = 1 / sq; a *= sq; b *= sq; c *= sq;}
        var d = Math.sin(angle), e = Math.cos(angle), f = 1 - e,
            g = mat[0],  h = mat[1], i = mat[2],  j = mat[3],
            k = mat[4],  l = mat[5], m = mat[6],  n = mat[7],
            o = mat[8],  p = mat[9], q = mat[10], r = mat[11],
            s = a * a * f + e,
            t = b * a * f + c * d,
            u = c * a * f - b * d,
            v = a * b * f - c * d,
            w = b * b * f + e,
            x = c * b * f + a * d,
            y = a * c * f + b * d,
            z = b * c * f - a * d,
            A = c * c * f + e;
        if(angle){
            if(mat != dest){
                dest[12] = mat[12]; dest[13] = mat[13];
                dest[14] = mat[14]; dest[15] = mat[15];
            }
        } else {
            dest = mat;
        }
        dest[0]  = g * s + k * t + o * u;
        dest[1]  = h * s + l * t + p * u;
        dest[2]  = i * s + m * t + q * u;
        dest[3]  = j * s + n * t + r * u;
        dest[4]  = g * v + k * w + o * x;
        dest[5]  = h * v + l * w + p * x;
        dest[6]  = i * v + m * w + q * x;
        dest[7]  = j * v + n * w + r * x;
        dest[8]  = g * y + k * z + o * A;
        dest[9]  = h * y + l * z + p * A;
        dest[10] = i * y + m * z + q * A;
        dest[11] = j * y + n * z + r * A;
        return dest;
    };
    this.lookAt = function(eye, center, up, dest){
        var eyeX    = eye[0],    eyeY    = eye[1],    eyeZ    = eye[2],
            upX     = up[0],     upY     = up[1],     upZ     = up[2],
            centerX = center[0], centerY = center[1], centerZ = center[2];
        if(eyeX == centerX && eyeY == centerY && eyeZ == centerZ){return this.identity(dest);}
        var x0, x1, x2, y0, y1, y2, z0, z1, z2, l;
        z0 = eyeX - center[0]; z1 = eyeY - center[1]; z2 = eyeZ - center[2];
        l = 1 / Math.sqrt(z0 * z0 + z1 * z1 + z2 * z2);
        z0 *= l; z1 *= l; z2 *= l;
        x0 = upY * z2 - upZ * z1;
        x1 = upZ * z0 - upX * z2;
        x2 = upX * z1 - upY * z0;
        l = Math.sqrt(x0 * x0 + x1 * x1 + x2 * x2);
        if(!l){
            x0 = 0; x1 = 0; x2 = 0;
        } else {
            l = 1 / l;
            x0 *= l; x1 *= l; x2 *= l;
        }
        y0 = z1 * x2 - z2 * x1; y1 = z2 * x0 - z0 * x2; y2 = z0 * x1 - z1 * x0;
        l = Math.sqrt(y0 * y0 + y1 * y1 + y2 * y2);
        if(!l){
            y0 = 0; y1 = 0; y2 = 0;
        } else {
            l = 1 / l;
            y0 *= l; y1 *= l; y2 *= l;
        }
        dest[0] = x0; dest[1] = y0; dest[2]  = z0; dest[3]  = 0;
        dest[4] = x1; dest[5] = y1; dest[6]  = z1; dest[7]  = 0;
        dest[8] = x2; dest[9] = y2; dest[10] = z2; dest[11] = 0;
        dest[12] = -(x0 * eyeX + x1 * eyeY + x2 * eyeZ);
        dest[13] = -(y0 * eyeX + y1 * eyeY + y2 * eyeZ);
        dest[14] = -(z0 * eyeX + z1 * eyeY + z2 * eyeZ);
        dest[15] = 1;
        return dest;
    };
    this.perspective = function(fovy, aspect, near, far, dest){
        var t = near * Math.tan(fovy * Math.PI / 360);
        var r = t * aspect;
        var a = r * 2, b = t * 2, c = far - near;
        dest[0]  = near * 2 / a;
        dest[1]  = 0;
        dest[2]  = 0;
        dest[3]  = 0;
        dest[4]  = 0;
        dest[5]  = near * 2 / b;
        dest[6]  = 0;
        dest[7]  = 0;
        dest[8]  = 0;
        dest[9]  = 0;
        dest[10] = -(far + near) / c;
        dest[11] = -1;
        dest[12] = 0;
        dest[13] = 0;
        dest[14] = -(far * near * 2) / c;
        dest[15] = 0;
        return dest;
    };
    this.ortho = function(left, right, top, bottom, near, far, dest) {
        var h = (right - left);
        var v = (top - bottom);
        var d = (far - near);
        dest[0]  = 2 / h;
        dest[1]  = 0;
        dest[2]  = 0;
        dest[3]  = 0;
        dest[4]  = 0;
        dest[5]  = 2 / v;
        dest[6]  = 0;
        dest[7]  = 0;
        dest[8]  = 0;
        dest[9]  = 0;
        dest[10] = -2 / d;
        dest[11] = 0;
        dest[12] = -(left + right) / h;
        dest[13] = -(top + bottom) / v;
        dest[14] = -(far + near) / d;
        dest[15] = 1;
        return dest;
    };
    this.transpose = function(mat, dest){
        dest[0]  = mat[0];  dest[1]  = mat[4];
        dest[2]  = mat[8];  dest[3]  = mat[12];
        dest[4]  = mat[1];  dest[5]  = mat[5];
        dest[6]  = mat[9];  dest[7]  = mat[13];
        dest[8]  = mat[2];  dest[9]  = mat[6];
        dest[10] = mat[10]; dest[11] = mat[14];
        dest[12] = mat[3];  dest[13] = mat[7];
        dest[14] = mat[11]; dest[15] = mat[15];
        return dest;
    };
    this.inverse = function(mat, dest){
        var a = mat[0],  b = mat[1],  c = mat[2],  d = mat[3],
            e = mat[4],  f = mat[5],  g = mat[6],  h = mat[7],
            i = mat[8],  j = mat[9],  k = mat[10], l = mat[11],
            m = mat[12], n = mat[13], o = mat[14], p = mat[15],
            q = a * f - b * e, r = a * g - c * e,
            s = a * h - d * e, t = b * g - c * f,
            u = b * h - d * f, v = c * h - d * g,
            w = i * n - j * m, x = i * o - k * m,
            y = i * p - l * m, z = j * o - k * n,
            A = j * p - l * n, B = k * p - l * o,
            ivd = 1 / (q * B - r * A + s * z + t * y - u * x + v * w);
        dest[0]  = ( f * B - g * A + h * z) * ivd;
        dest[1]  = (-b * B + c * A - d * z) * ivd;
        dest[2]  = ( n * v - o * u + p * t) * ivd;
        dest[3]  = (-j * v + k * u - l * t) * ivd;
        dest[4]  = (-e * B + g * y - h * x) * ivd;
        dest[5]  = ( a * B - c * y + d * x) * ivd;
        dest[6]  = (-m * v + o * s - p * r) * ivd;
        dest[7]  = ( i * v - k * s + l * r) * ivd;
        dest[8]  = ( e * A - f * y + h * w) * ivd;
        dest[9]  = (-a * A + b * y - d * w) * ivd;
        dest[10] = ( m * u - n * s + p * q) * ivd;
        dest[11] = (-i * u + j * s - l * q) * ivd;
        dest[12] = (-e * z + f * x - g * w) * ivd;
        dest[13] = ( a * z - b * x + c * w) * ivd;
        dest[14] = (-m * t + n * r - o * q) * ivd;
        dest[15] = ( i * t - j * r + k * q) * ivd;
        return dest;
    };
}

function qtnIV(){
    this.create = function(){
        return new Float32Array(4);
    };
    this.identity = function(dest){
        dest[0] = 0; dest[1] = 0; dest[2] = 0; dest[3] = 1;
        return dest;
    };
    this.inverse = function(qtn, dest){
        dest[0] = -qtn[0];
        dest[1] = -qtn[1];
        dest[2] = -qtn[2];
        dest[3] =  qtn[3];
        return dest;
    };
    this.normalize = function(dest){
        var x = dest[0], y = dest[1], z = dest[2], w = dest[3];
        var l = Math.sqrt(x * x + y * y + z * z + w * w);
        if(l === 0){
            dest[0] = 0;
            dest[1] = 0;
            dest[2] = 0;
            dest[3] = 0;
        }else{
            l = 1 / l;
            dest[0] = x * l;
            dest[1] = y * l;
            dest[2] = z * l;
            dest[3] = w * l;
        }
        return dest;
    };
    this.multiply = function(qtn1, qtn2, dest){
        var ax = qtn1[0], ay = qtn1[1], az = qtn1[2], aw = qtn1[3];
        var bx = qtn2[0], by = qtn2[1], bz = qtn2[2], bw = qtn2[3];
        dest[0] = ax * bw + aw * bx + ay * bz - az * by;
        dest[1] = ay * bw + aw * by + az * bx - ax * bz;
        dest[2] = az * bw + aw * bz + ax * by - ay * bx;
        dest[3] = aw * bw - ax * bx - ay * by - az * bz;
        return dest;
    };
    this.rotate = function(angle, axis, dest){
        var sq = Math.sqrt(axis[0] * axis[0] + axis[1] * axis[1] + axis[2] * axis[2]);
        if(!sq){return null;}
        var a = axis[0], b = axis[1], c = axis[2];
        if(sq != 1){sq = 1 / sq; a *= sq; b *= sq; c *= sq;}
        var s = Math.sin(angle * 0.5);
        dest[0] = a * s;
        dest[1] = b * s;
        dest[2] = c * s;
        dest[3] = Math.cos(angle * 0.5);
        return dest;
    };
    this.toVecIII = function(vec, qtn, dest){
        var qp = this.create();
        var qq = this.create();
        var qr = this.create();
        this.inverse(qtn, qr);
        qp[0] = vec[0];
        qp[1] = vec[1];
        qp[2] = vec[2];
        this.multiply(qr, qp, qq);
        this.multiply(qq, qtn, qr);
        dest[0] = qr[0];
        dest[1] = qr[1];
        dest[2] = qr[2];
        return dest;
    };
    this.toMatIV = function(qtn, dest){
        var x = qtn[0], y = qtn[1], z = qtn[2], w = qtn[3];
        var x2 = x + x, y2 = y + y, z2 = z + z;
        var xx = x * x2, xy = x * y2, xz = x * z2;
        var yy = y * y2, yz = y * z2, zz = z * z2;
        var wx = w * x2, wy = w * y2, wz = w * z2;
        dest[0]  = 1 - (yy + zz);
        dest[1]  = xy - wz;
        dest[2]  = xz + wy;
        dest[3]  = 0;
        dest[4]  = xy + wz;
        dest[5]  = 1 - (xx + zz);
        dest[6]  = yz - wx;
        dest[7]  = 0;
        dest[8]  = xz - wy;
        dest[9]  = yz + wx;
        dest[10] = 1 - (xx + yy);
        dest[11] = 0;
        dest[12] = 0;
        dest[13] = 0;
        dest[14] = 0;
        dest[15] = 1;
        return dest;
    };
    this.slerp = function(qtn1, qtn2, time, dest){
        var ht = qtn1[0] * qtn2[0] + qtn1[1] * qtn2[1] + qtn1[2] * qtn2[2] + qtn1[3] * qtn2[3];
        var hs = 1.0 - ht * ht;
        if(hs <= 0.0){
            dest[0] = qtn1[0];
            dest[1] = qtn1[1];
            dest[2] = qtn1[2];
            dest[3] = qtn1[3];
        }else{
            hs = Math.sqrt(hs);
            if(Math.abs(hs) < 0.0001){
                dest[0] = (qtn1[0] * 0.5 + qtn2[0] * 0.5);
                dest[1] = (qtn1[1] * 0.5 + qtn2[1] * 0.5);
                dest[2] = (qtn1[2] * 0.5 + qtn2[2] * 0.5);
                dest[3] = (qtn1[3] * 0.5 + qtn2[3] * 0.5);
            }else{
                var ph = Math.acos(ht);
                var pt = ph * time;
                var t0 = Math.sin(ph - pt) / hs;
                var t1 = Math.sin(pt) / hs;
                dest[0] = qtn1[0] * t0 + qtn2[0] * t1;
                dest[1] = qtn1[1] * t0 + qtn2[1] * t1;
                dest[2] = qtn1[2] * t0 + qtn2[2] * t1;
                dest[3] = qtn1[3] * t0 + qtn2[3] * t1;
            }
        }
        return dest;
    };
}

function torus(row, column, irad, orad, color){
    var pos = new Array(), nor = new Array(),
        col = new Array(), st  = new Array(), idx = new Array();
    for(var i = 0; i <= row; i++){
        var r = Math.PI * 2 / row * i;
        var rr = Math.cos(r);
        var ry = Math.sin(r);
        for(var ii = 0; ii <= column; ii++){
            var tr = Math.PI * 2 / column * ii;
            var tx = (rr * irad + orad) * Math.cos(tr);
            var ty = ry * irad;
            var tz = (rr * irad + orad) * Math.sin(tr);
            var rx = rr * Math.cos(tr);
            var rz = rr * Math.sin(tr);
            if(color){
                var tc = color;
            }else{
                tc = hsva(360 / column * ii, 1, 1, 1);
            }
            var rs = 1 / column * ii;
            var rt = 1 / row * i + 0.5;
            if(rt > 1.0){rt -= 1.0;}
            rt = 1.0 - rt;
            pos.push(tx, ty, tz);
            nor.push(rx, ry, rz);
            col.push(tc[0], tc[1], tc[2], tc[3]);
            st.push(rs, rt);
        }
    }
    for(i = 0; i < row; i++){
        for(ii = 0; ii < column; ii++){
            r = (column + 1) * i + ii;
            idx.push(r, r + column + 1, r + 1);
            idx.push(r + column + 1, r + column + 2, r + 1);
        }
    }
    return {p : pos, n : nor, c : col, t : st, i : idx};
}

function sphere(row, column, rad, color){
    var pos = new Array(), nor = new Array(),
        col = new Array(), st  = new Array(), idx = new Array();
    for(var i = 0; i <= row; i++){
        var r = Math.PI / row * i;
        var ry = Math.cos(r);
        var rr = Math.sin(r);
        for(var ii = 0; ii <= column; ii++){
            var tr = Math.PI * 2 / column * ii;
            var tx = rr * rad * Math.cos(tr);
            var ty = ry * rad;
            var tz = rr * rad * Math.sin(tr);
            var rx = rr * Math.cos(tr);
            var rz = rr * Math.sin(tr);
            if(color){
                var tc = color;
            }else{
                tc = hsva(360 / row * i, 1, 1, 1);
            }
            pos.push(tx, ty, tz);
            nor.push(rx, ry, rz);
            col.push(tc[0], tc[1], tc[2], tc[3]);
            st.push(1 - 1 / column * ii, 1 / row * i);
        }
    }
    r = 0;
    for(i = 0; i < row; i++){
        for(ii = 0; ii < column; ii++){
            r = (column + 1) * i + ii;
            idx.push(r, r + 1, r + column + 2);
            idx.push(r, r + column + 2, r + column + 1);
        }
    }
    return {p : pos, n : nor, c : col, t : st, i : idx};
}

function cube(side, color){
    var hs = side * 0.5;
    var pos = [
        -hs, -hs,  hs,  hs, -hs,  hs,  hs,  hs,  hs, -hs,  hs,  hs,
        -hs, -hs, -hs, -hs,  hs, -hs,  hs,  hs, -hs,  hs, -hs, -hs,
        -hs,  hs, -hs, -hs,  hs,  hs,  hs,  hs,  hs,  hs,  hs, -hs,
        -hs, -hs, -hs,  hs, -hs, -hs,  hs, -hs,  hs, -hs, -hs,  hs,
         hs, -hs, -hs,  hs,  hs, -hs,  hs,  hs,  hs,  hs, -hs,  hs,
        -hs, -hs, -hs, -hs, -hs,  hs, -hs,  hs,  hs, -hs,  hs, -hs
    ];
    var nor = [
        -1.0, -1.0,  1.0,  1.0, -1.0,  1.0,  1.0,  1.0,  1.0, -1.0,  1.0,  1.0,
        -1.0, -1.0, -1.0, -1.0,  1.0, -1.0,  1.0,  1.0, -1.0,  1.0, -1.0, -1.0,
        -1.0,  1.0, -1.0, -1.0,  1.0,  1.0,  1.0,  1.0,  1.0,  1.0,  1.0, -1.0,
        -1.0, -1.0, -1.0,  1.0, -1.0, -1.0,  1.0, -1.0,  1.0, -1.0, -1.0,  1.0,
         1.0, -1.0, -1.0,  1.0,  1.0, -1.0,  1.0,  1.0,  1.0,  1.0, -1.0,  1.0,
        -1.0, -1.0, -1.0, -1.0, -1.0,  1.0, -1.0,  1.0,  1.0, -1.0,  1.0, -1.0
    ];
    var col = new Array();
    for(var i = 0; i < pos.length / 3; i++){
        if(color){
            var tc = color;
        }else{
            tc = hsva(360 / pos.length / 3 * i, 1, 1, 1);
        }
        col.push(tc[0], tc[1], tc[2], tc[3]);
    }
    var st = [
        0.0, 0.0, 1.0, 0.0, 1.0, 1.0, 0.0, 1.0,
        0.0, 0.0, 1.0, 0.0, 1.0, 1.0, 0.0, 1.0,
        0.0, 0.0, 1.0, 0.0, 1.0, 1.0, 0.0, 1.0,
        0.0, 0.0, 1.0, 0.0, 1.0, 1.0, 0.0, 1.0,
        0.0, 0.0, 1.0, 0.0, 1.0, 1.0, 0.0, 1.0,
        0.0, 0.0, 1.0, 0.0, 1.0, 1.0, 0.0, 1.0
    ];
    var idx = [
         0,  1,  2,  0,  2,  3,
         4,  5,  6,  4,  6,  7,
         8,  9, 10,  8, 10, 11,
        12, 13, 14, 12, 14, 15,
        16, 17, 18, 16, 18, 19,
        20, 21, 22, 20, 22, 23
    ];
    return {p : pos, n : nor, c : col, t : st, i : idx};
}

function hsva(h, s, v, a){
    if(s > 1 || v > 1 || a > 1){return;}
    var th = h % 360;
    var i = Math.floor(th / 60);
    var f = th / 60 - i;
    var m = v * (1 - s);
    var n = v * (1 - s * f);
    var k = v * (1 - s * (1 - f));
    var color = new Array();
    if(!s > 0 && !s < 0){
        color.push(v, v, v, a); 
    } else {
        var r = new Array(v, n, m, m, k, v);
        var g = new Array(k, v, v, n, m, m);
        var b = new Array(m, m, k, v, v, n);
        color.push(r[i], g[i], b[i], a);
    }
    return color;
}