图形学中折射refract函数推导

概述

上一篇文章我们给大家介绍了图形学中的反射定律原文，这次我们大家介绍的图形学中折射函数的原理，refract函数的数学意义。

折射是光线从一种介质传播到另一种介质时发生的现象。当光线在不同折射率的介质之间传播时，它会改变其传播方向。这是由于光在不同介质中的传播速度不同所引起的。

大家可以看看这个视频

斯涅尔定律（又称为折射定律）

根据斯涅尔定律（又称为折射定律），维基百科，入射光线与法线的夹角与折射光线与法线的夹角之间存在一定的关系。这个关系可以用下面的公式表示：

$$ n1 * sin(θ1) = n2 * sin(θ2) $$

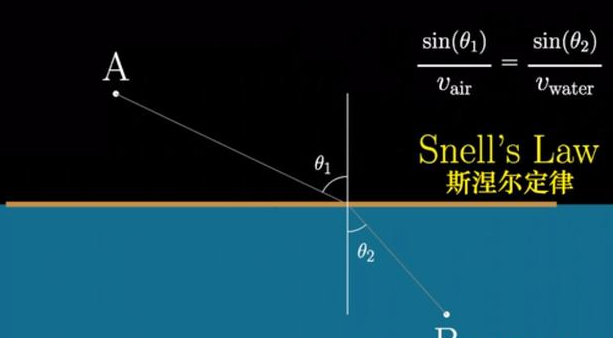
其中，n1和n2分别代表两种介质的折射率，θ1是入射角（入射光线与法线的夹角），θ2是折射角（折射光线与法线的夹角）。

当光从一个介质传播到另一个折射率较高的介质时，折射角会小于入射角，光线向法线靠拢。而当光从一个介质传播到另一个折射率较低的介质时，折射角会大于入射角，光线离开法线。

折射现象在许多日常生活中的情况中都可以观察到，比如当光线从空气进入水中或玻璃中时，就会发生折射。这也是为什么在看到水中的物体时，它们的位置看起来更高，因为光线被水的折射效应所影响。

公式推导

float refract(float I, float N, float eta) 这个式子是我们再glsl语言中经常调用的函数，该函数是折射原理的封装。

首先我们要明确自己的目标还有已知的一些条件信息：

条件：已知 I（入射光线向量） 、N（法线向量）、还有eta指定折射率的比率

目的：根据已知条件推断出折射光线的方向和大小。

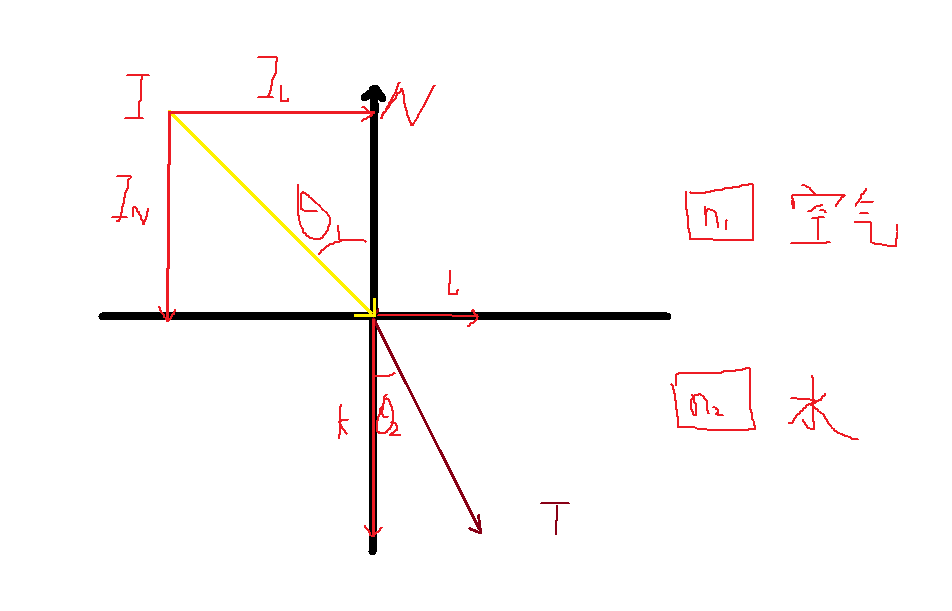
步骤一：我们先反向推导，如果求反射光线T，其公式如下所示：

$$ T=k+l $$

步骤二：计算k

$$ \begin{aligned}k&=-|k|\cdot N\\&=-(T\cdot N)\cdot N\\&=-（|T||N|cos\theta_2）\cdot N\\&=-cos\theta_2\cdot N\end{aligned} $$

注：此时我们假设 I（入射光线向量） 、N（法线向量）和T（反射光线向量）长度均为1的向量，也就是单位向量。

步骤三：计算l

$$ l=|l|\cdot\widehat{l} $$

注：任何一个向量都可以表示为该向量的模乘上该向量的单位向量，也就是方向向量。

接下来我们分别求该向量的模与该向量的方向向量。

$$ |l|=sin\theta_2\cdot|T|=sin\theta_2\cdot1 = sin\theta_2 $$

下面是求l向量的方向向量，由下图可知我们l的方向向量就是水平向量，我们可以转换为求I_{l}的方向向量。

$$ l=|l|\cdot\frac{I_l}{|I_l|} $$

那么

$$ |I_{l}|=sin\theta_{1} $$

再求I_{l}

$$ \begin{array}{c}{I_{l}=I-I_{N}}\\{=I-(I\cdot N)\cdot N}\end{array} $$

$$ I_{N}=-(|I|cos\theta_{1})\cdot N = -(|I||N|cos\theta_{1})\cdot N= -(I\cdot N)\cdot N $$

所以我们最终带入下面公式：

$$ l=|l|\cdot\frac{I_l}{|I_l|} =sin\theta_{2}\cdot{\frac{I-(I\cdot N)\cdot N}{sin\theta_{1}}} $$

步骤四：

步骤三得到的公式中还有theta_{2},根据斯涅尔定律

$$ n_1sin\theta_1=n_2sin\theta_2 $$

得到

$$ sin\theta_{2}=\frac{n_{1}sin\theta_{1}}{n_{2}} $$

再根据三角函数公式：

$$ (sin\theta_1)^2=1-(cos\theta_1)^2 $$

又已知：

$$ cos\theta_1=N\cdot I $$

所以：

$$ (sin\theta_{1})^{2}=1-(cos\theta_{1})^{2}=1-(N\cdot I)^{2} $$

所以：

$$ \begin{aligned} cos\theta_{2}& =\sqrt{1-(\frac{n_{1}sin\theta_{1}}{n_{2}})^{2}} \\ &=\sqrt{1-\frac{n_1^2}{n_2^2}[1-(N\cdot I)^2]} \end{aligned} $$

最终我们可以得到：

$$ \begin{gathered} \text{T} =-N\cdot\sqrt{1-\frac{n_{1}^{2}}{n_{2}^{2}}[1-(N\cdot I)^{2}]}+\frac{n_{1}}{n_{2}}\cdot[I-(I\cdot N)\cdot N] \\ =-\left(\frac{n_{1}}{n_{2}}N\cdot I+\sqrt{1-\frac{n_{1}^{2}}{n_{2}^{2}}[1-(N\cdot I)^{2}]}\right)N+\frac{n_{1}}{n_{2}}I \end{gathered} $$

下面是我们对上述数学公式的代码实现：

vec3 refract(const vec3 &I, const vec3 &N, const float &ior)
{
    float cosi = clamp(-1, 1, dotProduct(I, N));
    float etai = 1, etat = ior;
    vec3 n = N;
    if (cosi < 0) { cosi = -cosi; } else { std::swap(etai, etat); n= -N; }
    float eta = etai / etat;
    float k = 1 - eta * eta * (1 - cosi * cosi);
    return k < 0 ? 0 : eta * I + (eta * cosi - sqrtf(k)) * n;
}

参考文献

https://www.bilibili.com/video/BV1yN4y137tz/?spm_id_from=333.337.search-card.all.click&vd_source=01ae3fc576acbf5bd3e59f3307bb594f