数学中的导数与梯度的基础概念理解
背景
梯度本质是数学里的概念,但是它在图形学领域应用极广。通常用于计算图像或三维场景中各个位置的颜色、光照、纹理等属性的变化率。以下是梯度在图形学中的一些应用:
- 纹理映射:梯度可以用于计算纹理映射中的变化率,从而实现更加真实的纹理渲染效果。
- 着色:在光照和材质表面属性计算中,梯度可以用于计算每个像素的光照强度和阴影效果,从而实现更加逼真的着色。
- 图像处理:在图像处理中,梯度可以用于检测边缘和纹理等特征,从而实现图像分割、特征提取和图像增强等功能。
- 面部识别:在面部识别中,梯度可以用于计算人脸图像中不同部位的颜色、纹理和亮度等属性的变化率,从而实现更加准确的人脸识别。
- 物体追踪:在物体追踪中,梯度可以用于计算目标物体的移动方向和速度,从而实现更加精准的物体追踪。
当然在其他领域还有很多应用...我们今天来浅聊一下梯度这一概念.....
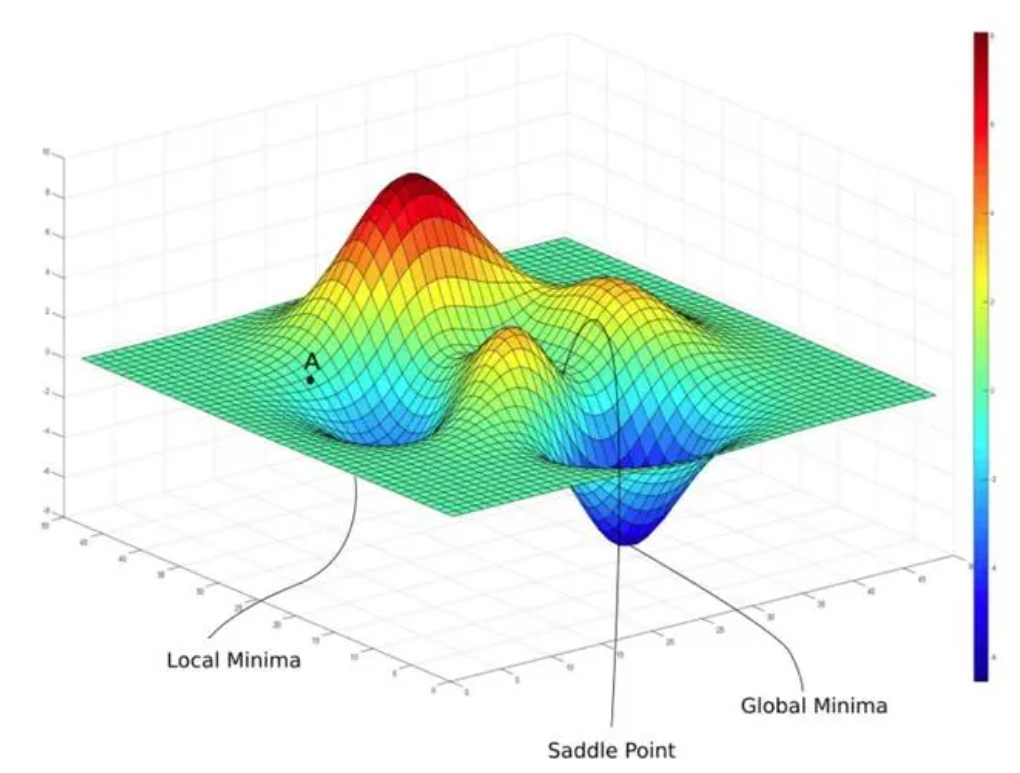
提到梯度,就必须从导数(derivative)、偏导数(partial derivative)和方向导数(directional derivative)讲起,弄清楚这些概念,才能够正确理解为什么在优化问题中使用梯度下降法来优化目标函数,并熟练掌握梯度下降法(Gradient Descent)。
| 概念 | 物理意义 |
|---|---|
| 导数 | 函数在该点的瞬时变化率 |
| 偏导数 | 函数在坐标轴方向上的变化率 |
| 方向导数 | 函数在某点沿某个特定方向的变化率 |
| 梯度 | 函数在该点一个函数在某个点上的变化率和方向 |
导数
导数就是函数在某个点处的瞬时斜率,也可以理解为函数在这个点处的切线的斜率。下面就是求某一函数在某一点处的变化率
$$ f'(x_{0} ) = \lim_{\Delta x \to 0} = \frac{\mathrm{\Delta } y}{\mathrm{\Delta } x}Δx是x的变化量 Δy是函数的增量; $$
偏导数
定义
$$ \frac { \partial } { \partial x _ { j } } f ( x _ { 0 } , x _ { 1 } , \ldots , x _ { n } ) = \operatorname { lim } _ { \Delta x \rightarrow 0 } \frac { \Delta y } { \Delta x } = \operatorname { lim } _ { \Delta x \rightarrow 0 } \frac { f ( x _ { 0 } , \ldots , x _ { j } + \Delta x , \ldots , x _ { n } ) - f ( x _ { 0 } , \ldots , x _ { j } , \ldots , x _ { n } ) } { \Delta x } $$
可以看到,导数与偏导数本质是一致的,都是当自变量的变化量趋于0 时,函数值的变化量与自变量变化量比值的极限。直观地说,偏导数也就是函数在某一点上沿坐标轴正方向的的变化率。
注:区别在于:
导数,指的是一元函数中,函数 y=f(x)在某一点处沿 x轴正方向的变化率;
偏导数,指的是多元函数中,函数 f(x1,x2,…,xn)在某一点处沿某一坐标轴 (x1,x2,…,xn)正方向的变化率。
几何意义
偏导数 fx(x0,y0)就是曲面被平面 y=y0所截得的曲线在某点 处的切线,对 x轴的斜率
偏导数 fy(x0,y0) 就是曲面被平面 x=x0 所截得的曲线在某点 处的切线,对 y 轴的斜率

可能上述还比较抽象大家可以参考下b站这个视频
方向导数
方向导数可以用于描述一个函数在某个点上在不同方向上的变化率。很多时候要考虑多元函数沿任意方向的变化率,那么就引出了方向导数。方向导数的定义如下:
$$ \frac { \partial } { \partial l } f ( x _ { 0 } , x _ { 1 } , \ldots , x _ { n } ) = \operatorname { lim } _ { \rho \rightarrow 0 } \frac { \Delta y } { \Delta x } = \operatorname { lim } _ { \rho \rightarrow 0 } \frac { f ( x _ { 0 } + \Delta x _ { 0 } , \ldots , x _ { j } + \Delta x _ { j } , \ldots , x _ { n } + \Delta x _ { n } ) - f ( x _ { 0 } , \ldots , x _ { j } , \ldots , x _ { n } ) } { \rho } $$
$$ \rho = \sqrt { ( \Delta x _ { 0 } ) ^ { 2 } + \cdots + ( \Delta x _ { j } ) ^ { 2 } + \cdots + ( \Delta x _ { n } ) ^ { 2 } } $$
注:方向导数与偏导数的区别在,偏导数只描述函数在某个特定方向上的变化率,而方向导数可以描述函数在任意方向上的变化率。
梯度
定义
$$ \operatorname { grad } ( x _ { 0 } , x _ { 1 } , \ldots , x _ { n } ) = ( \frac { \partial f } { \partial x _ { 0 } } , \ldots , \frac { \partial f } { \partial x _ { j } } , \ldots , \frac { \partial f } { \partial x _ { n } } ) $$
梯度通常指的是某个函数在某个点上的斜率或导数。如果一个函数在某个点上的梯度是正的,那么它告诉你在该点上增加该函数的输入会使输出值增加;如果梯度为负,则减少输入会导致输出值增加。函数在某一点的梯度是这样一个向量,它的方向与取得最大方向导数的方向一致,而它的模为方向导数的最大值。
注:
- 梯度是一个向量,即有方向有大小;
- 梯度的方向是最大方向导数的方向;
- 梯度的值是最大方向导数的值。
今天就闲聊到这里后面,之所以写这篇关于数学基础文章是我们后续再根据光线追踪求法线的时候会用到梯度这一理论基础,后续我们继续来更新shader部分。



 shader
shader WebGL
WebGL cesium
cesium threeJS
threeJS gis
gis 模型
模型 glsl
glsl



