文档教程 - 文章中心 - 第2页 - ICE

发布文章

1 点赞

1433 浏览

202309官网更新：包括付费邀请提问和余额管理等功能的高级问答服务
官网更新 功能说明

地虎降天龙 2023-09-12

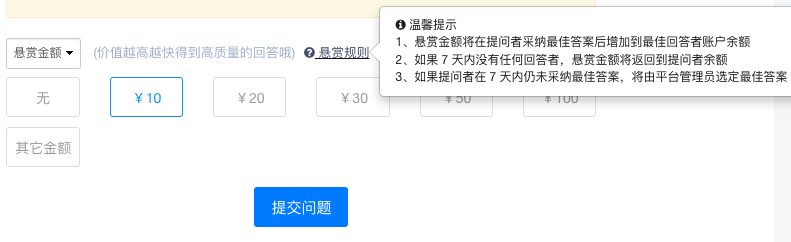
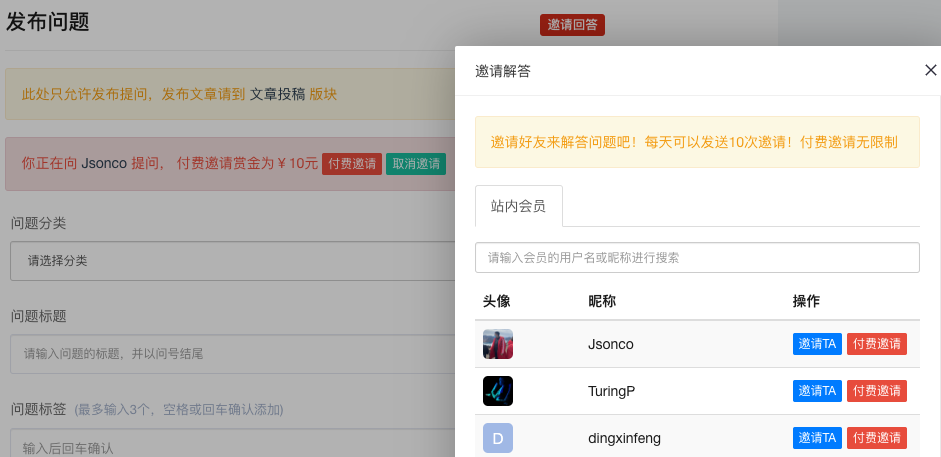
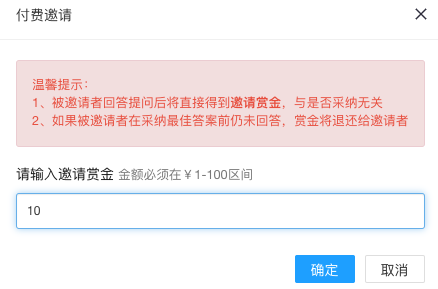
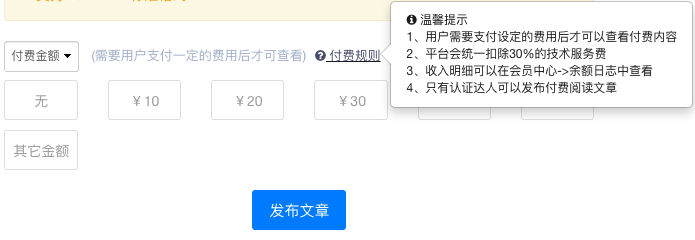
本次更新带来了令人期待已久的高级问答服务，包括付费邀请提问和余额管理等功能。我们旨在解决日常提问中遇到的难题或需要大量时间解决的问题。通过付费邀请提问，提问者可以为解答者提供适当的回报，从而促进社区的公平和活跃。

2 点赞

2325 浏览

UE5中UV坐标加减乘除基本变换原理浅析
UE5 UV坐标 UV坐标基本运算

sunny 2023-08-13

UE5中UV坐标是什么？作用是什么？为什么坐标轴加一个数，贴图反而向左？乘以一个数，贴图密度反而变大？本篇文章详细演示给你看，形象理解通俗易懂！

3 点赞

2148 浏览

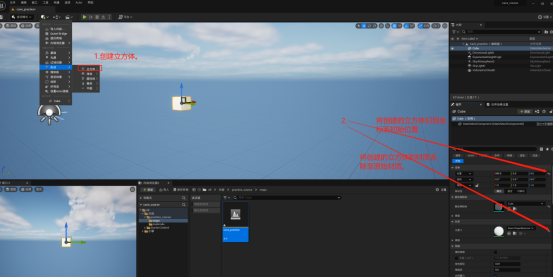
超详细讲解带你学习制作UE5案例之梦幻洞穴
UE5 超详细讲解UE5

sunny 2023-08-01

作者初心旨在通过超详细案例讲解，带大家更快更高效掌握UE5。从来的经历告诉我，但凡我会的东西再讲给别人，别人一定能懂。全程干货，速速跟上学习的脚步，一起轻松掌握ue5吧！

2 点赞

7173 浏览

超详细讲解UE5材质基础
UE5 UE5材质

sunny 2023-08-01

作者初心旨在通过超详细案例讲解，带大家更快更高效掌握UE5。本篇在上篇案例实践基础上，超详细系统讲解UE5材质基础知识。

0 点赞

2557 浏览

threejs+shader绘制太阳讲解
shader threeJS

Jsonco 2023-06-07

我们尝试用threejs+shader做一个关于太阳的案例，该案例的核心技术点在于noise的使用+threejsAPI的使用。

0 点赞

2251 浏览

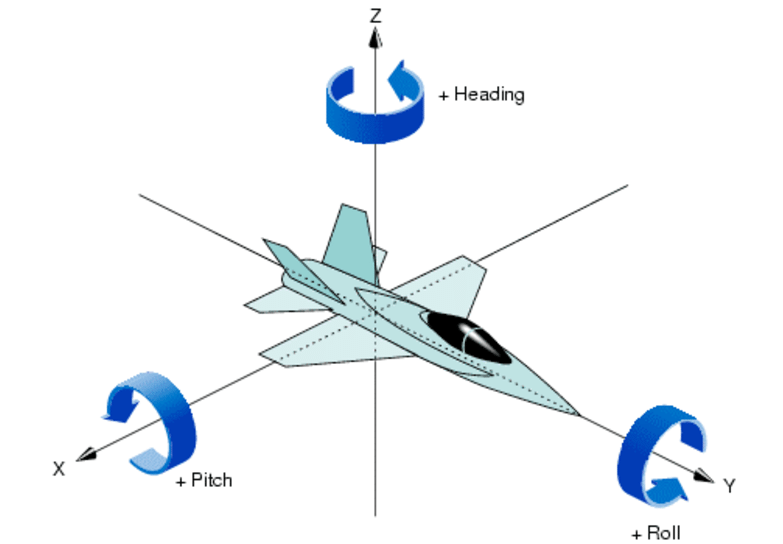
几何学——四元数基本概念
四元数

Jsonco 2023-06-04

在 3D 编程的世界中，有时数学知识非常重要。我们前面给大家讲过矩阵，矩阵能做很事情，但是矩阵同样具有着很多局限性，四元数实际上为了解决矩阵在某些方面的问题，而诞生的一种全新的数学表达式。接下来我们详细介绍下四元数。

0 点赞

1549 浏览

## 背景矩阵其实大家都不陌生了，本质是一个数学概念，这个概念本属于数学，但在图形学应用中就显得有些许问题。我们来这节内容就来专门聊聊矩阵的优点和缺点。 ## 优点 1. 矩阵操作很方便：矩阵可以作为一个整体来处理，可以进行加减乘除等各种运算，大大简化了计算过程。 2. 可以表示多维数据：矩阵可以表示任意维度的数据，例如二维或三维空间中的位置信息、图像像素或时间序列等。 3. 矩阵的形式被图形 API所使用。受到了前一节所述原因的影响，图形 API使用矩阵来描述方位。(API就是应

2 点赞

8951 浏览

几何学——矩阵基础知识汇总
几何学 图形学 数学

Jsonco 2023-05-05

这是一篇一看到底的文章，主要是全面剖析矩阵。众所周知，矩阵是一个由数值排列成的矩形阵列。矩阵在CG图形流水线中起着重要作用，你会在 3D 应用程序的代码中经常看到它们的使用。矩阵没有什么复杂的；如果你害怕它们，那可能是因为你还没有完全理解它们的工作机理。所以让我们来一起解决它，这篇文章我将会把所有关于矩阵的知识罗列出来。希望后续同学有关于矩阵的知识都可以在下面留言，不断丰富文章。

0 点赞

2920 浏览

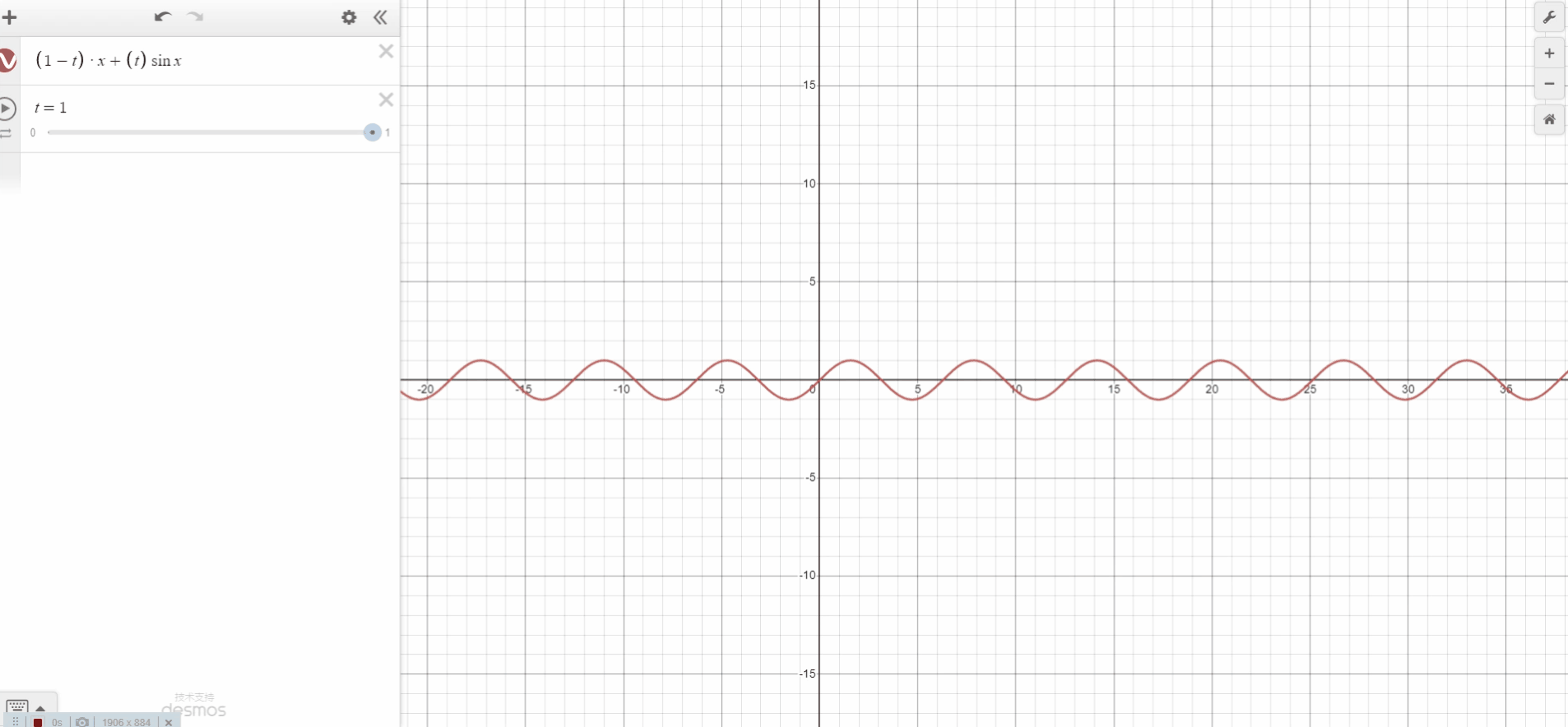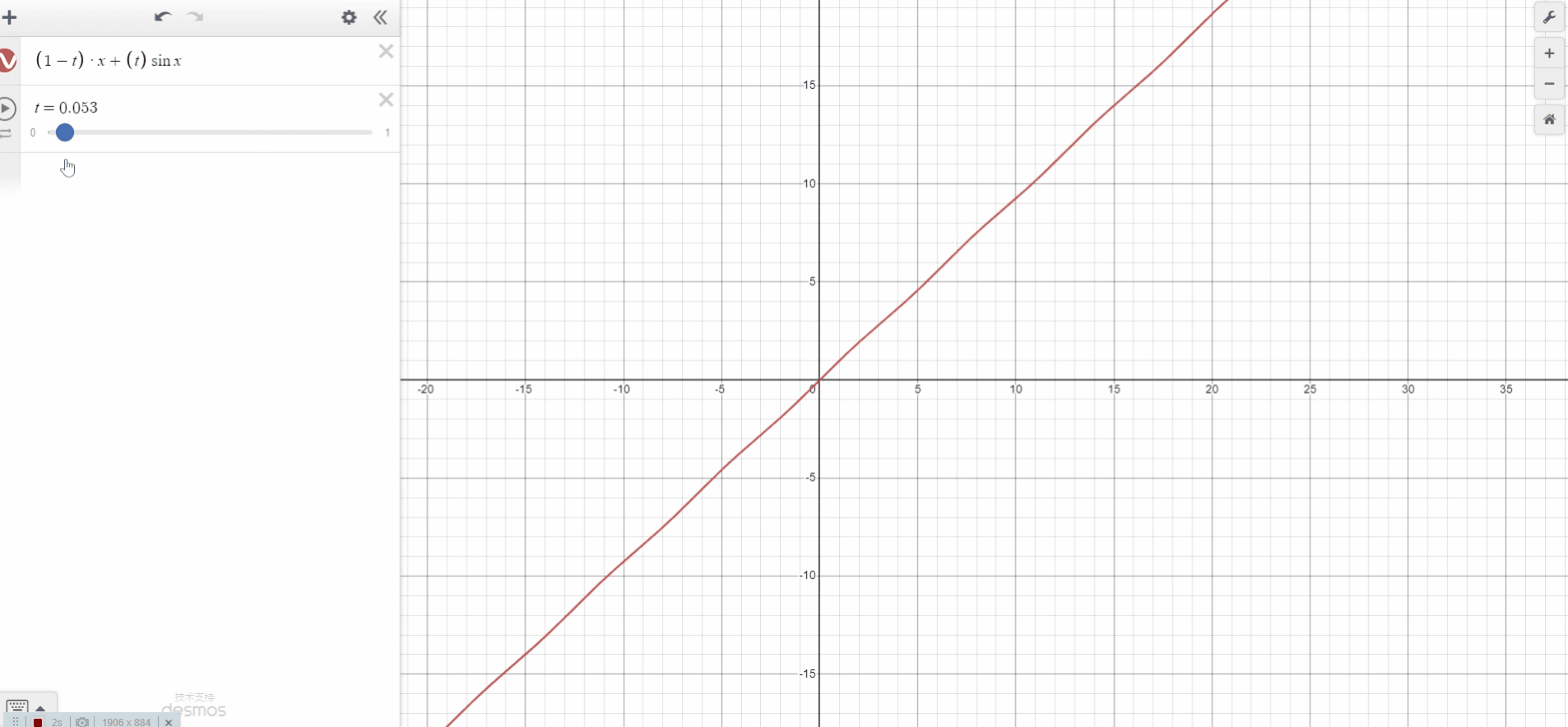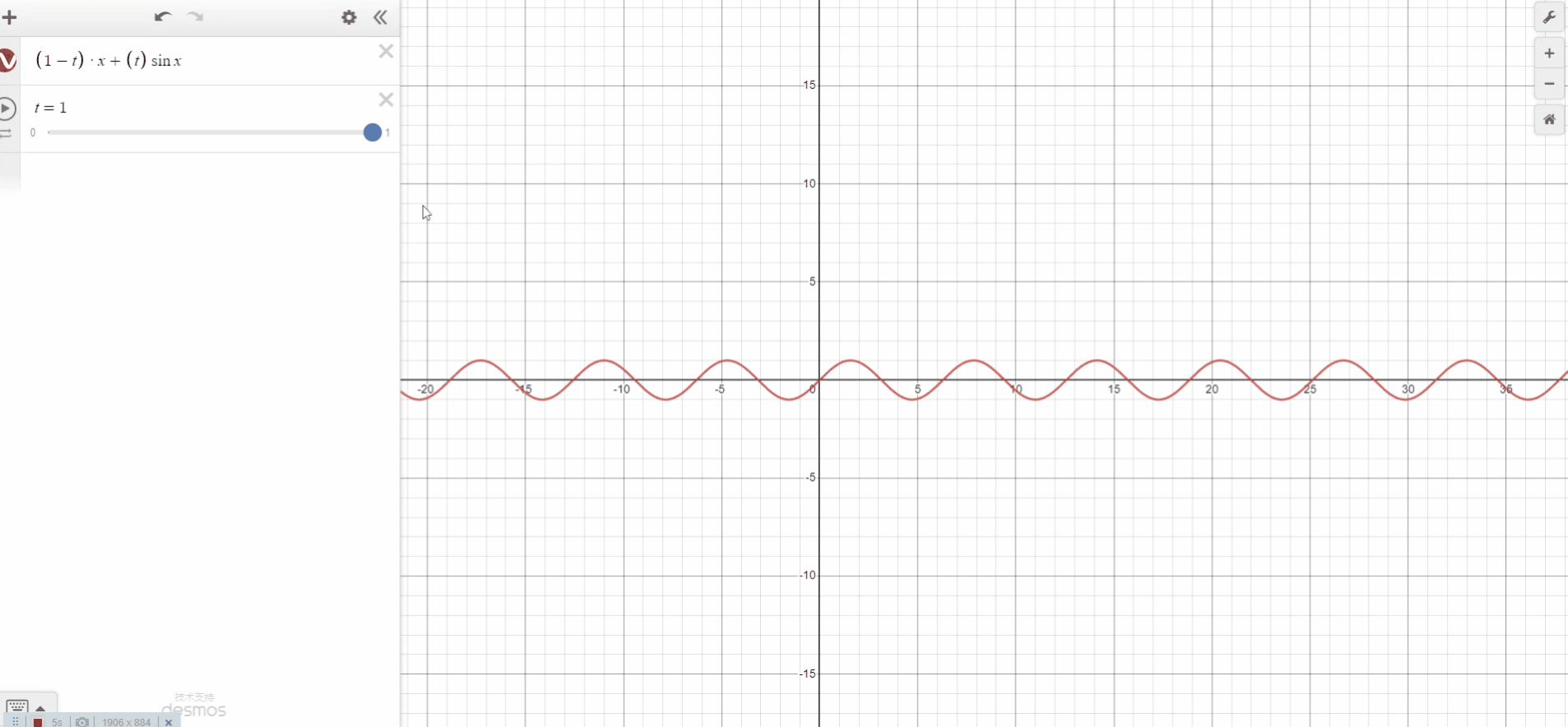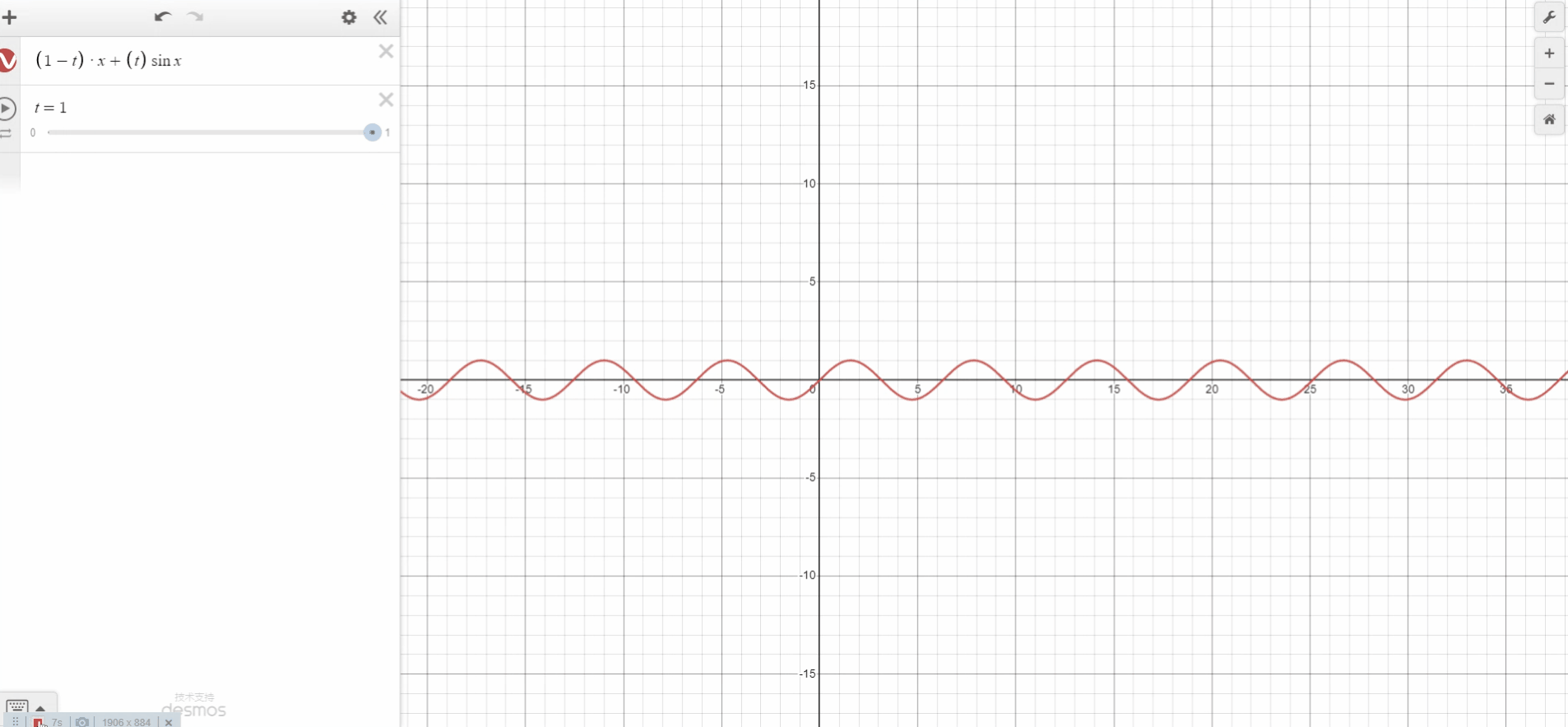
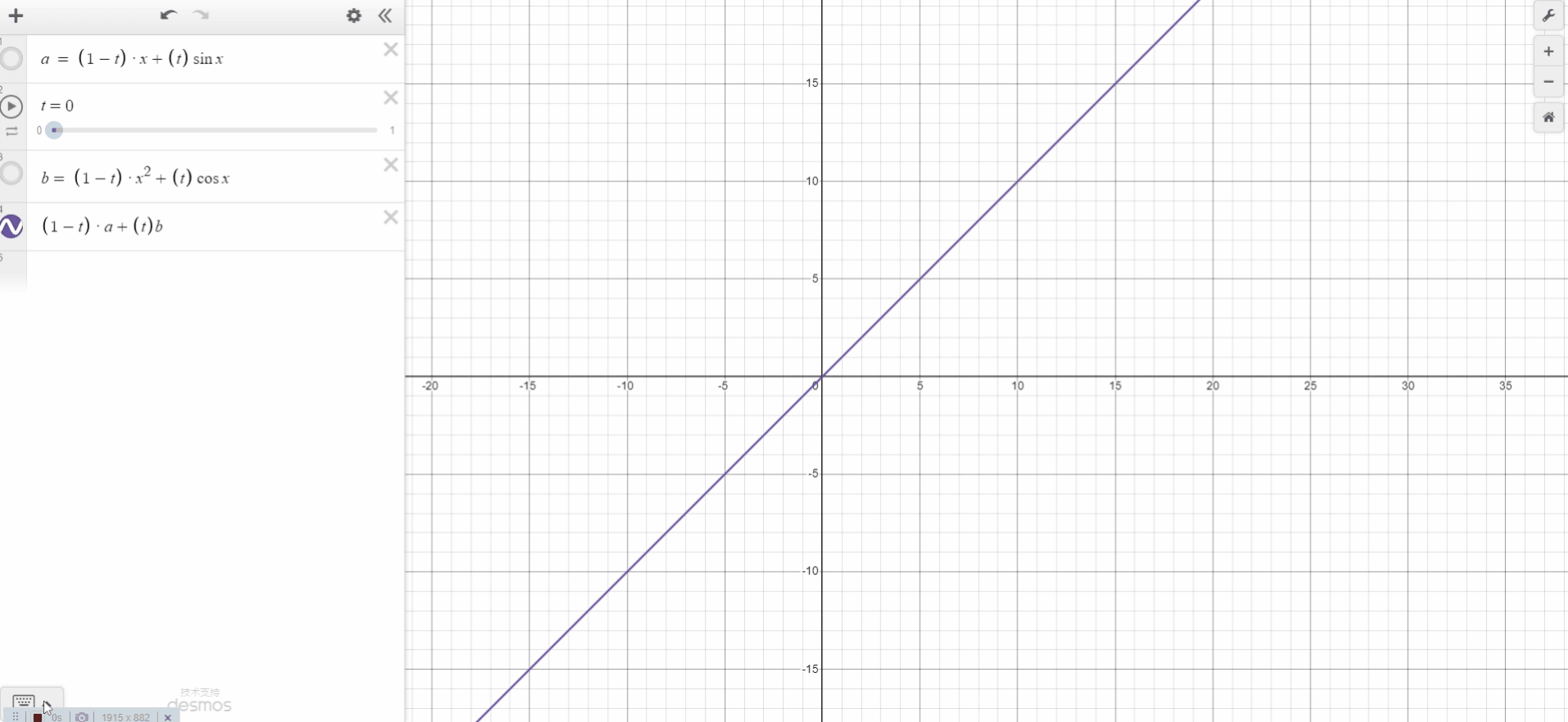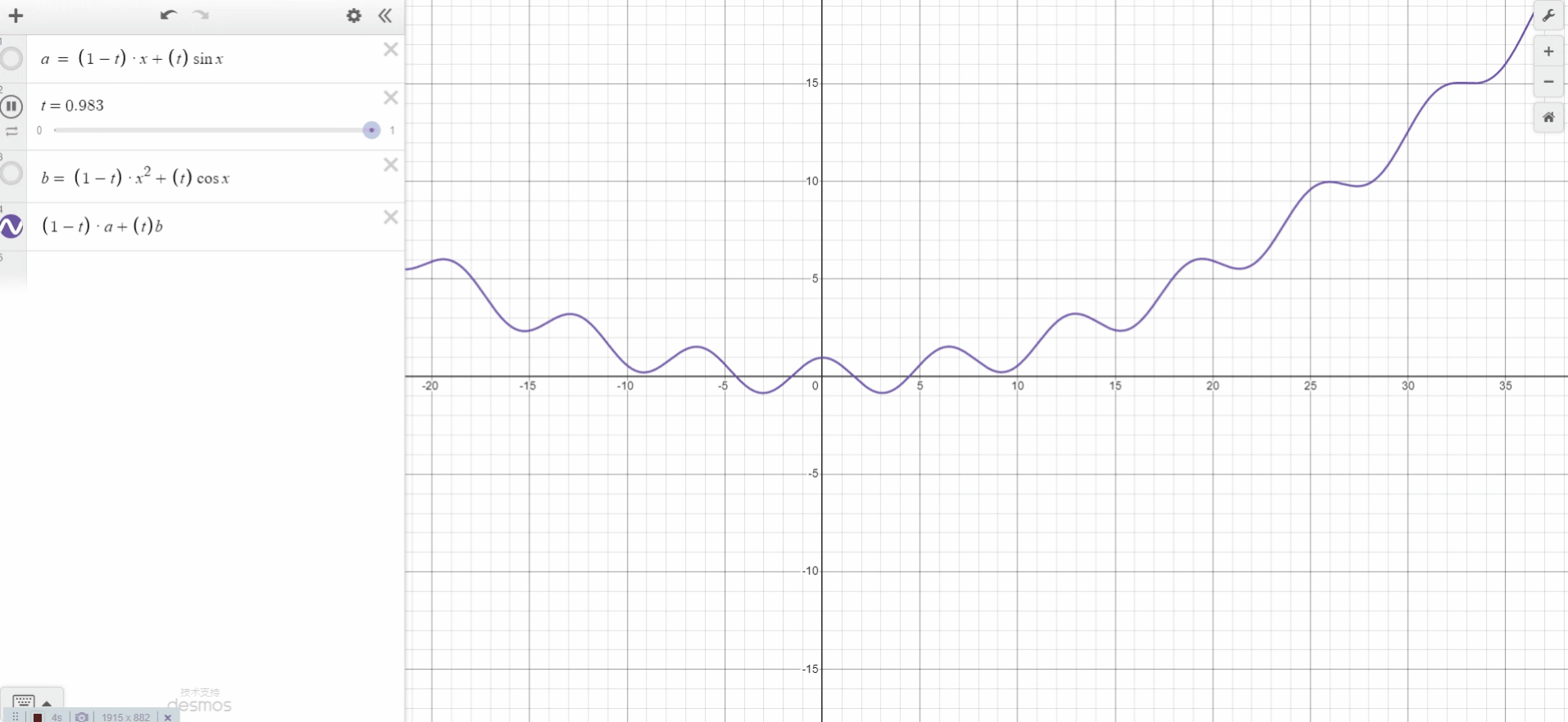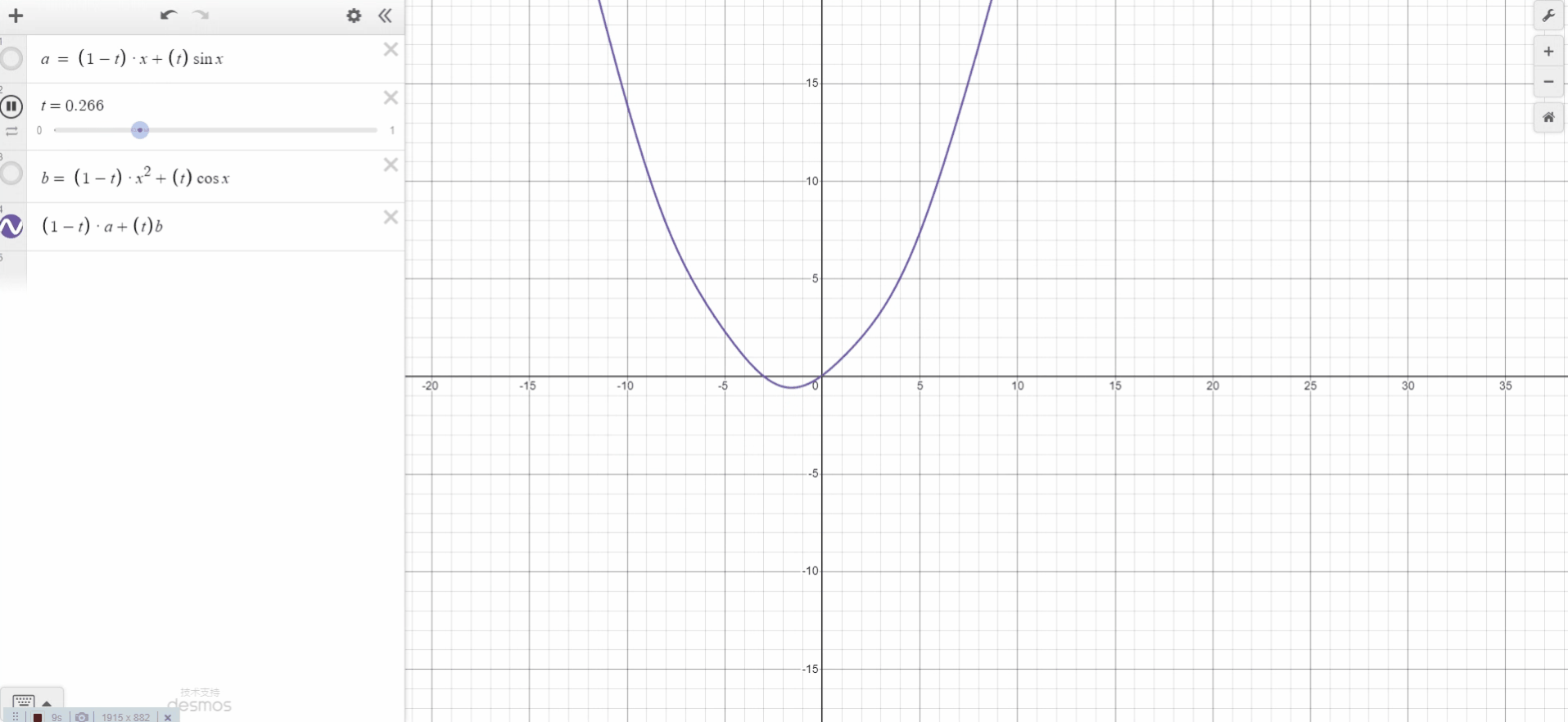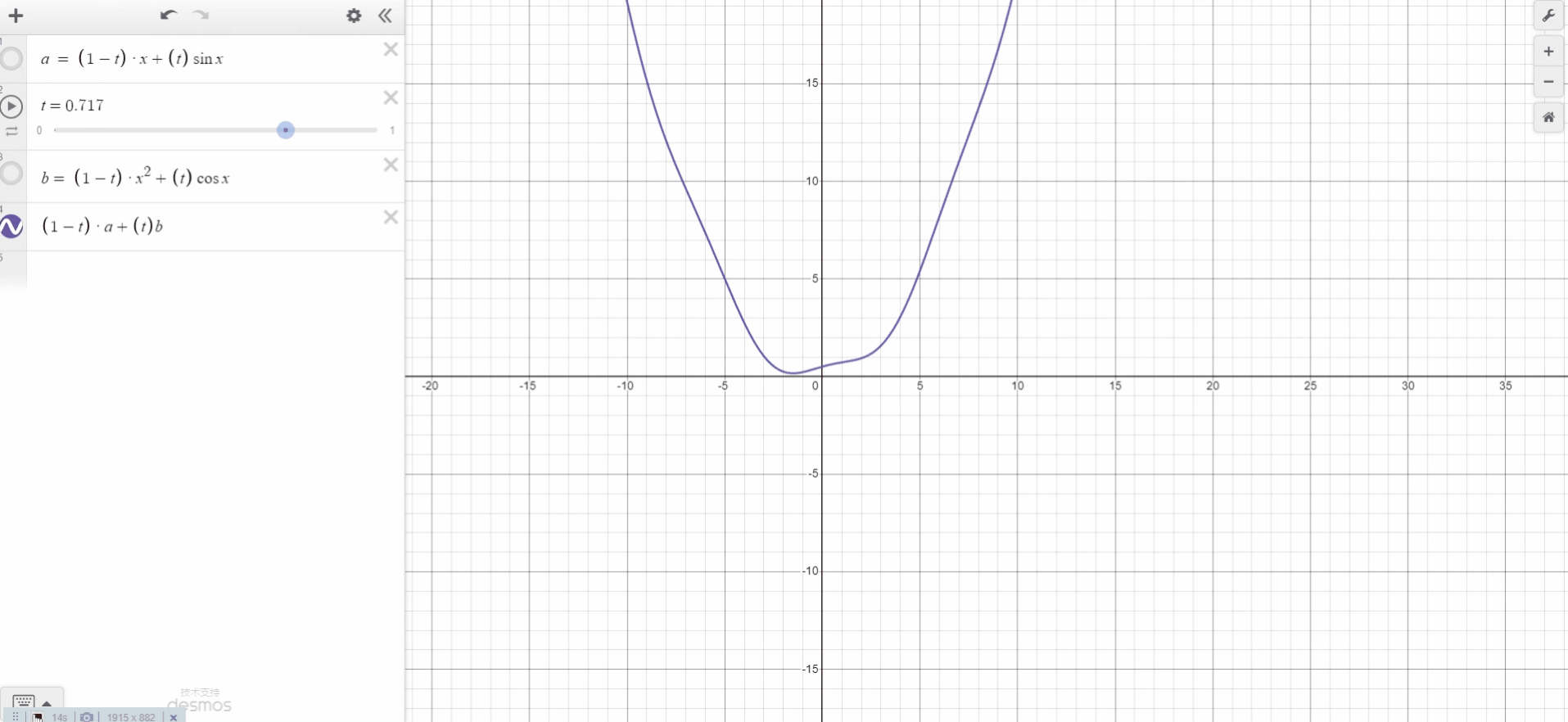
几何学——插值函数概括
几何学 图形学 数学

admin 2023-04-26

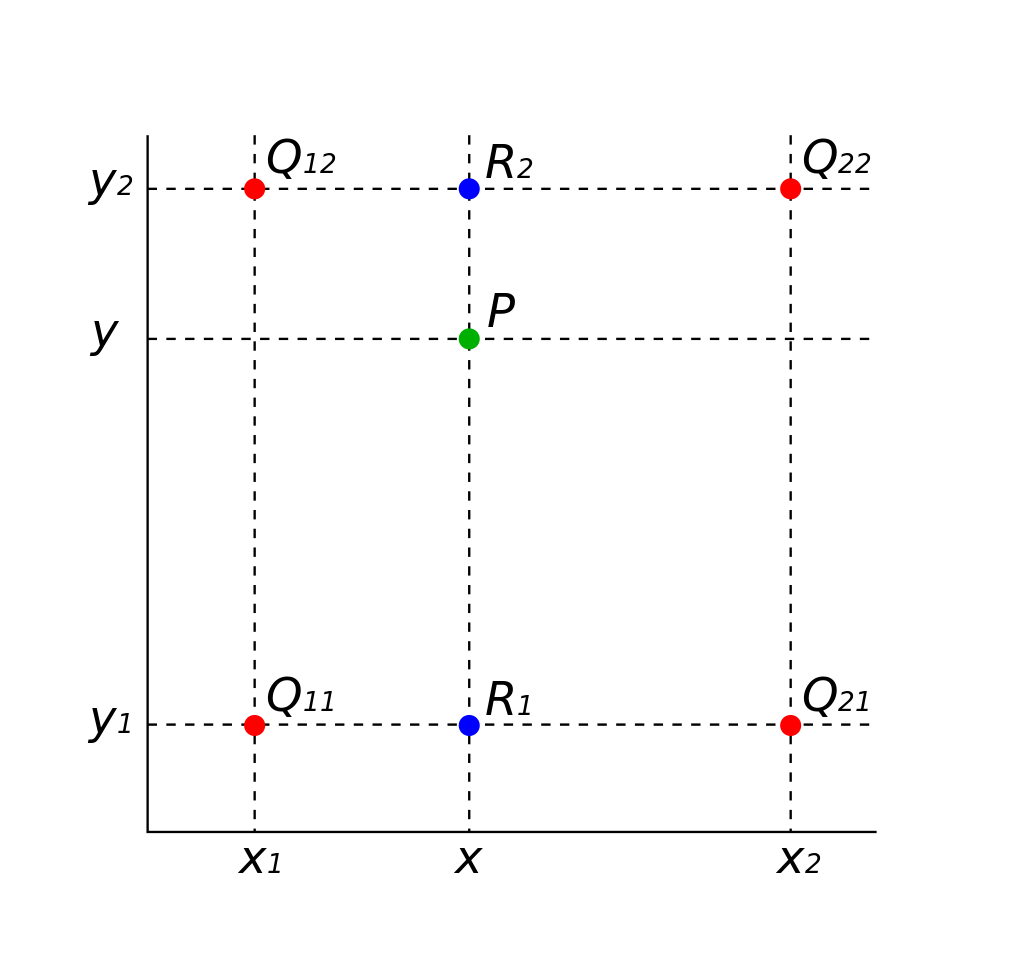
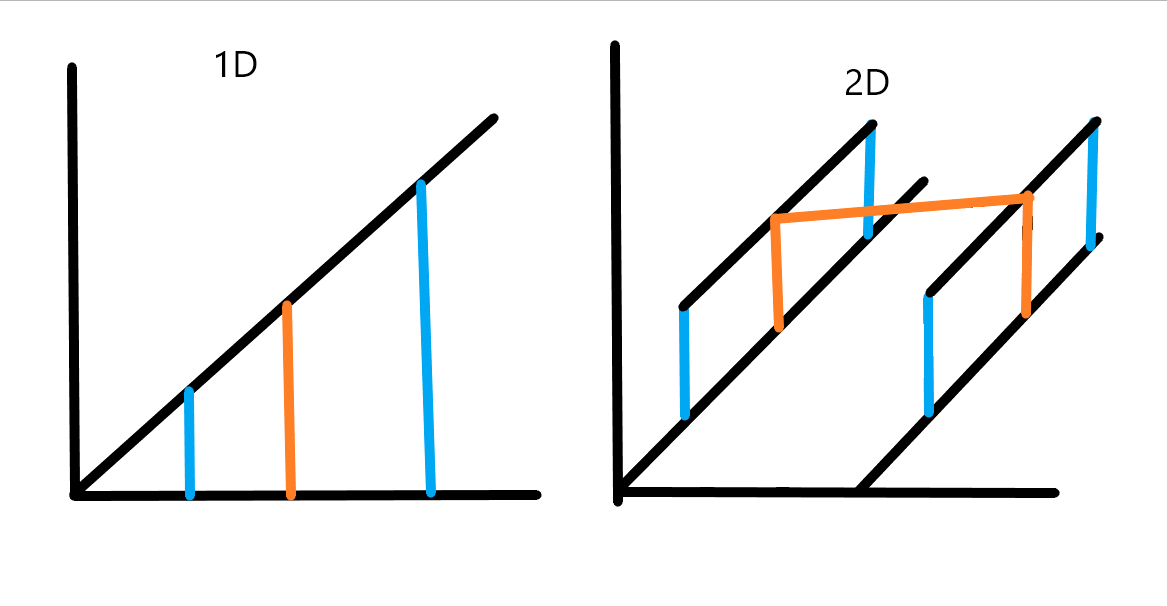
插值是计算机图形学中非常常用的技术。数据通常指定在规则网格上（已知 1D、2D 或 3D 网格的顶点位置），需要自动计算出其他随机位置的值。如果样本位于网格顶点，那么我们可以简单地使用存储在那里的值。但是，如果样本位于网格上的其他任何位置（单元格中的某个位置），那么考虑到我们在那里没有数据，我们需要通过对存储在单元格顶点的值求平均值来计算一个。这种技术称为插值。

0 点赞

5215 浏览