2 点赞
1 点赞
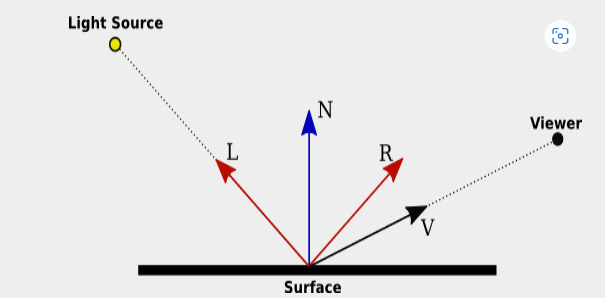
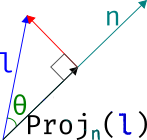
置顶 图形学中Phong高光反射公式数学推演
最近有小伙伴问我,在网上看了很多关于Phong模型中高光公式的推广,感觉越看越糊涂,并且很多都是错的,或者结果是对的但是中间推导基本是囫囵吞枣,搞得晕头转向。今天我们专门针对这个小知识点来做讲解。主要是数学知识的运用哈!
1 点赞
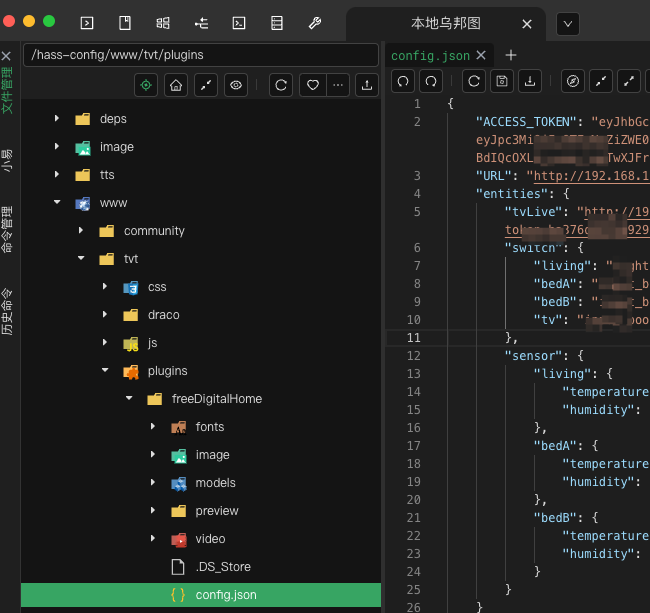
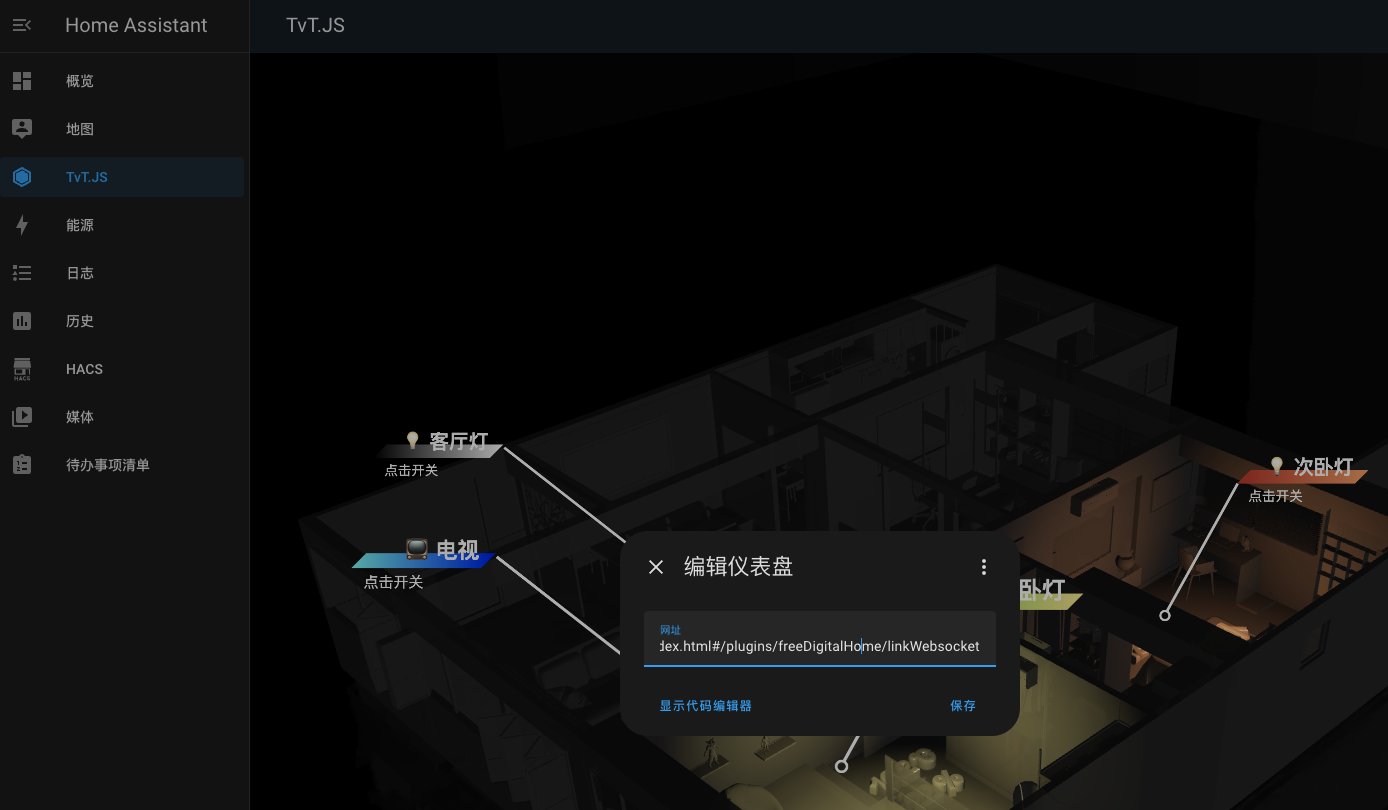
置顶 🎉🎉🎊 三维可视化项目快速落地の开源框架 🎊🎉🎉 TvT.js
旨在解决在国内通过Vue快速实现三维可视化项目的迅速落地的开源项目。采用的技术栈包括Vue.js、Three.js和Tres.js,致力于为开发者提供一个简便而强大的框架,以实现三维可视化项目的高效开发。
3 点赞
1 点赞
置顶 几何学——欧拉角与万向锁看这一篇就够了(含threejs demo演示)
依靠我的个人的理解以及我阅读了大量的文献,将欧拉角定义分解成了几个要点,方便大家理解:- 任意一个旋转都可以用相互垂直的三个轴来表示,这三个轴我们一般采用的是笛卡尔坐标系(其实任意轴都可以,只不过笛卡尔坐标系最有意义)- 旋转后,原来互相垂直的轴可能不再垂直,**当前步骤只能影响下一个旋转步骤,不能影响之前的旋转步骤**- 这里**默认右手坐标系,逆时针为正**,任意三个轴可以作为旋转轴。- 物体坐标系中我们称三个基本轴向叫(heading、pitch、bank);惯性坐标
0 点赞
2 点赞
几何学——矩阵基础知识汇总
这是一篇一看到底的文章,主要是全面剖析矩阵。众所周知,矩阵是一个由数值排列成的矩形阵列。矩阵在CG图形流水线中起着重要作用,你会在 3D 应用程序的代码中经常看到它们的使用。矩阵没有什么复杂的;如果你害怕它们,那可能是因为你还没有完全理解它们的工作机理。所以让我们来一起解决它,这篇文章我将会把所有关于矩阵的知识罗列出来。希望后续同学有关于矩阵的知识都可以在下面留言,不断丰富文章。
0 点赞
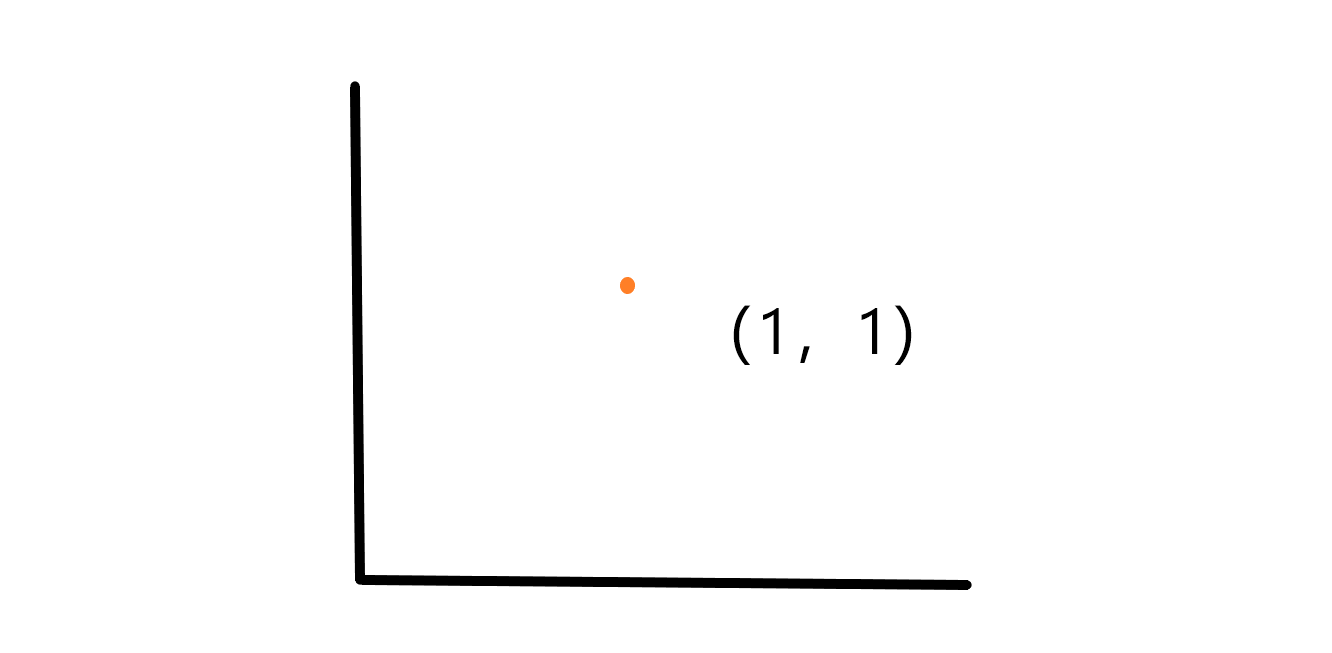
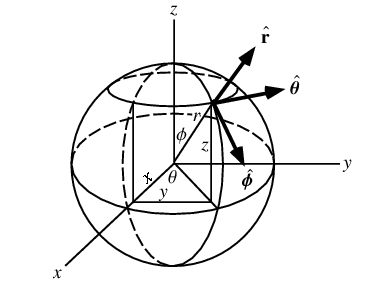
几何学——坐标系概括
坐标系是描述物体或点的位置和方向的一种数学工具。它由坐标轴和原点组成,通常用于二维或三维空间中。
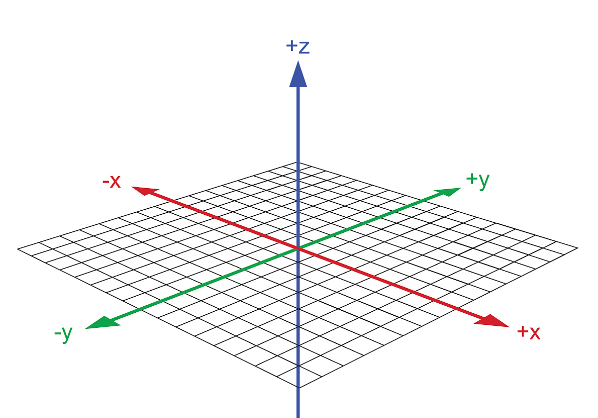
坐标轴是一条直线,其上有等距离的点,用来表示某个方向上的距离。在二维坐标系中,通常有两条垂直的坐标轴,即水平轴和垂直轴;在三维坐标系中,则需要增加一条竖直的轴。这些轴通常用 x、y 和 z 表示,并通过原点相交。
位置可以用一组数字(称为坐标)来描述。在二维坐标系中,每个点都有一个唯一的坐标,由它在水平轴和垂直轴上的位置确定。在三维坐标系中,每个点由它在三个轴上的位置确定。
坐标系不仅可以用
2 点赞
1 点赞
初步探讨一下Shader中的SDF应用
SDF在图形学里算是很基础的理论知识,并且在其上,衍生了很多复杂的知识体系。SDF定义虽然简单,但是正因为其简单,所以给我们后期编程带来很大的遍历性,其规律和特性具有很好的复用性,封装成相应的函数,我们可以直接复制、粘贴,运行就可以产生想要的效果。
0 点赞
1 点赞
1 点赞
npm 及 yarn 代理设置及更换为国内下载源
由于有时候网络的原因,会导致 npm 、yarn 下载遇到各种各样的问题。而且我们正好会使用科学上网方法。那么我们就可以为 npm 、yarn 设置代理。让它们通过代理的方式的得到更优的下载网络,从而解决疑难杂症。
0 点赞
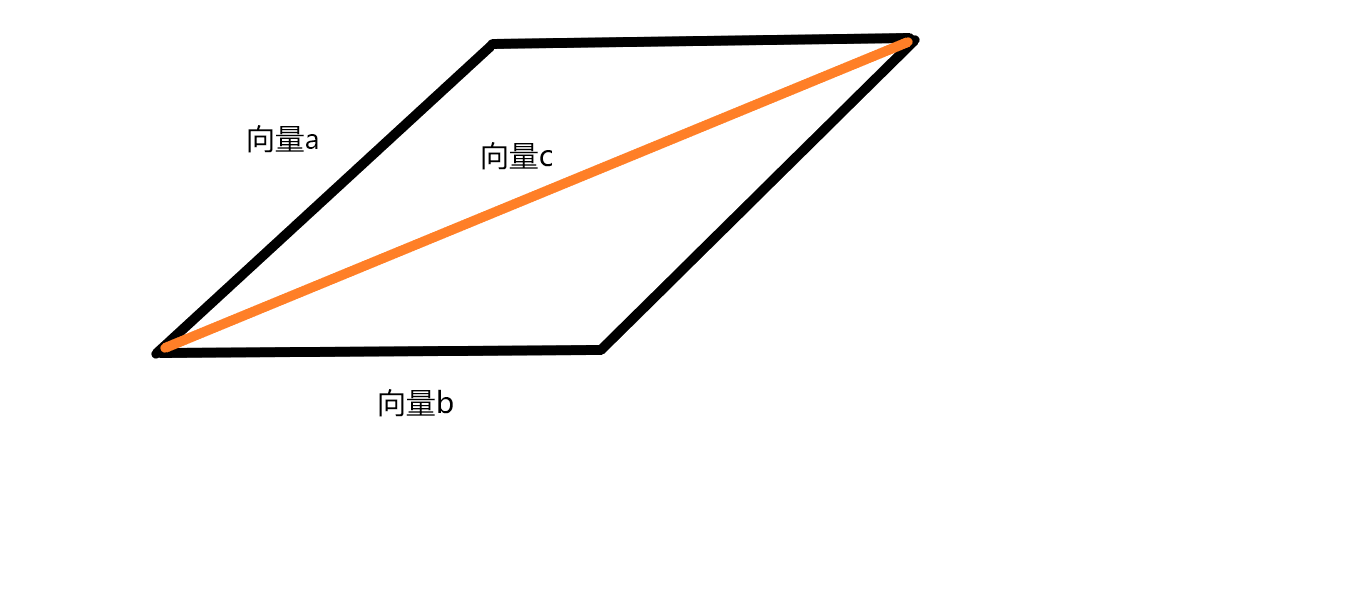
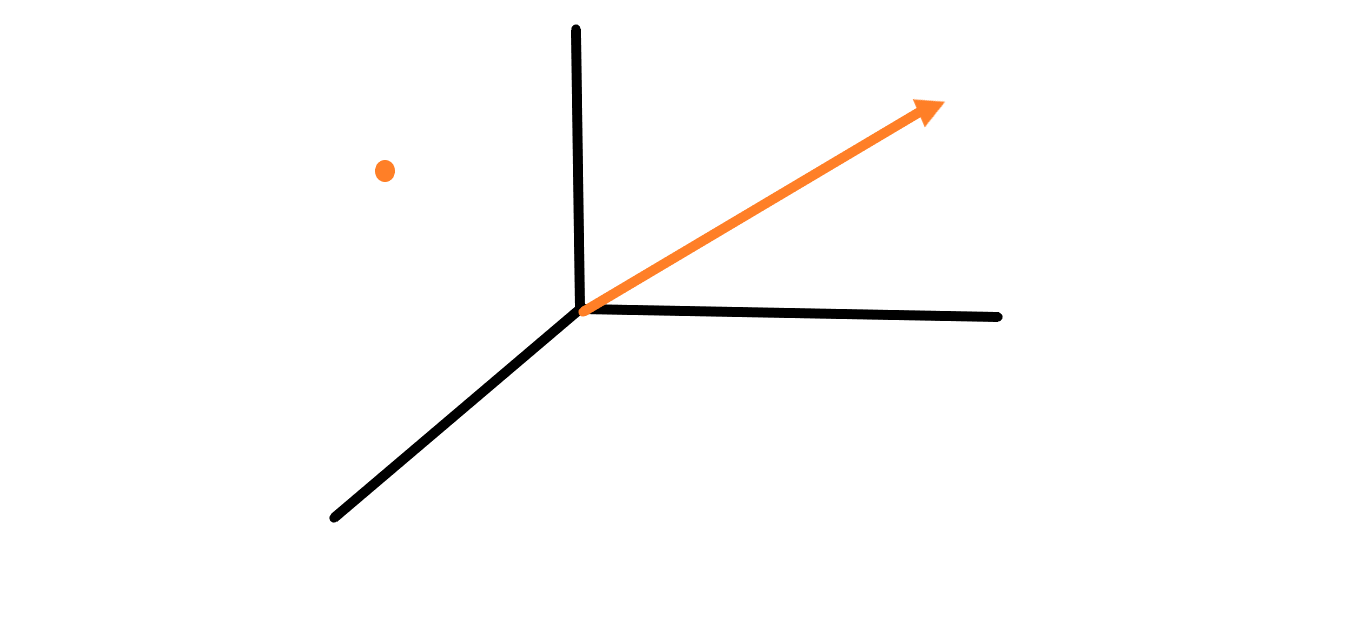
几何学——点、向量和法线
我们在webgl课程中给大家讲到了一定的数学知识,其实他并不是完整的,我们在很多应用实例中了解到,其实很多时候我们也可以不用线性代数,也可以实现。其实我们在之前课程中也定义过线性代数的“下里巴人”定义:**线性代数只不过是数学家定义的牢笼。-(没错冰哥我说的)**为什么这个牢笼不是你定义的呢,因为你不是牛逼的数学家,他们就是想制定一个规格化的数据组织标准,方便后面的数学推导和运算,恰巧的是我们计算机很喜欢这种规格化的数据格式,所以它被广泛应用到计算机图形学里面咯。
1 点赞
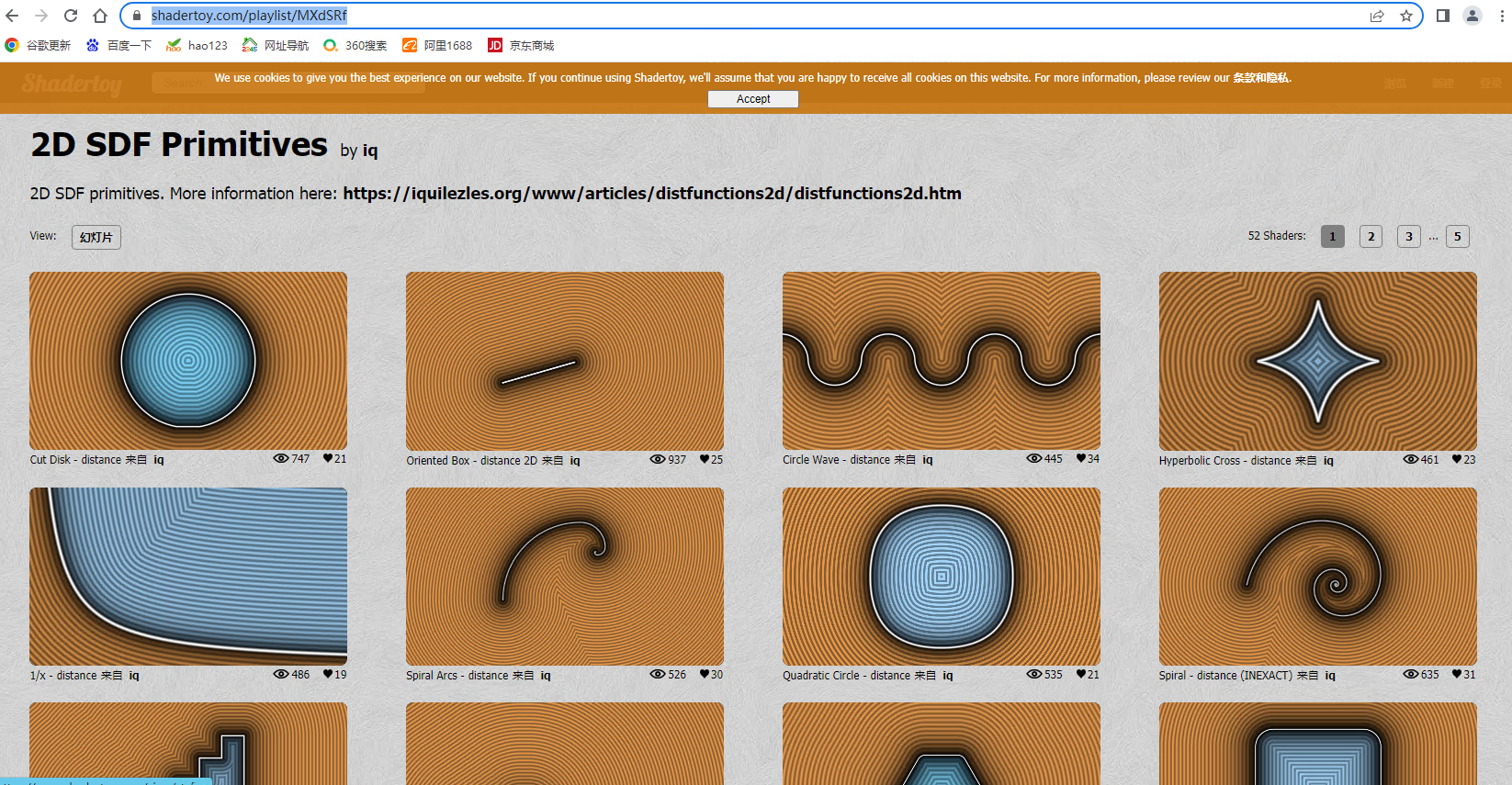
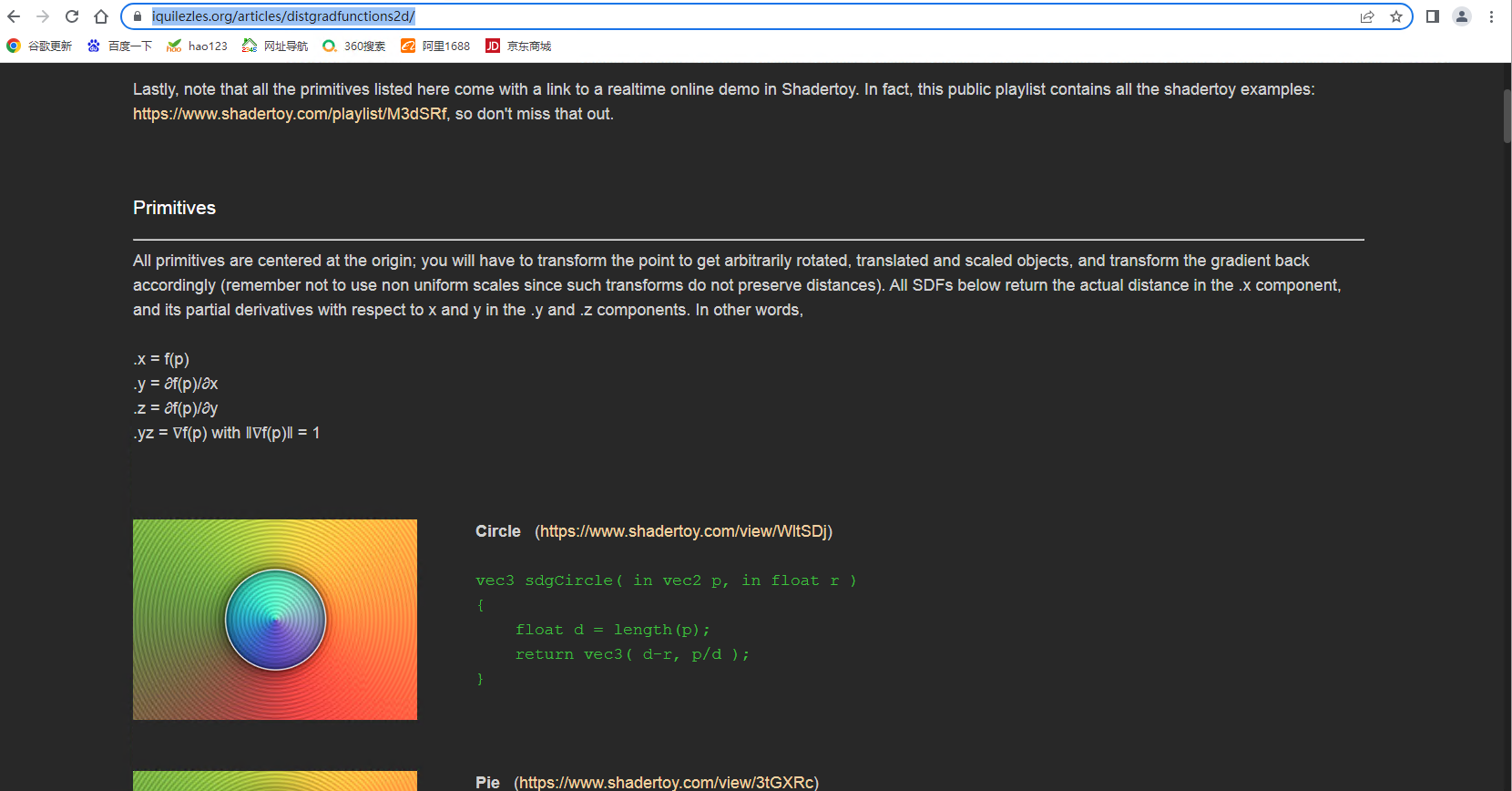
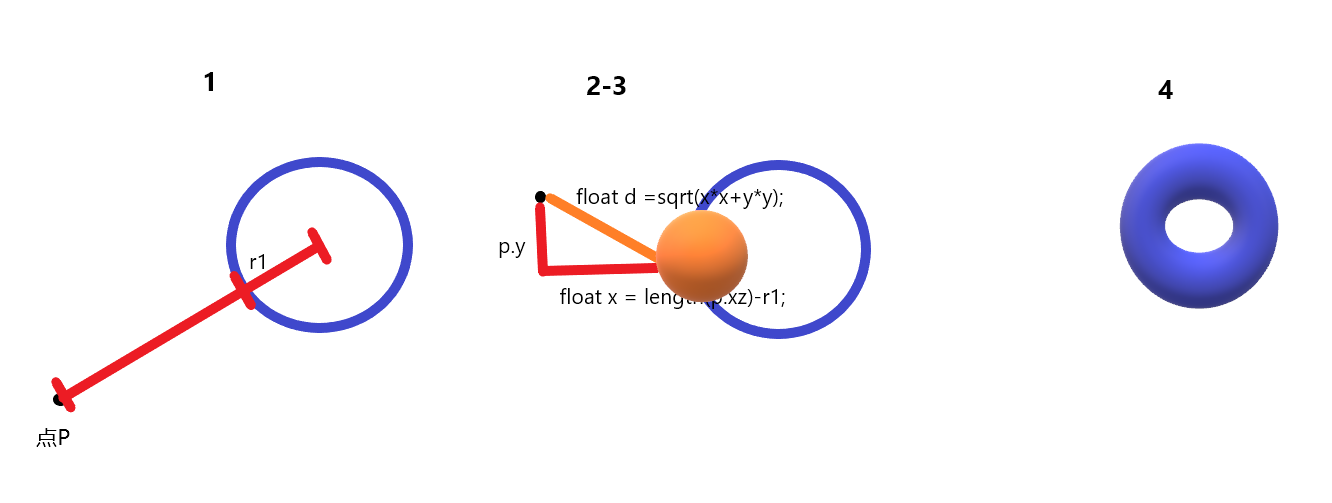
根据SDF绘制更多的三维形状(持续更新)
三维SDF,全称为三维有符号距离场(Signed Distance Field),是一种用于表示三维模型的方法。它将每个点到最近模型表面的距离作为该点的值,并根据其位置与模型表面的关系(在内部或外部)对其进行符号化处理。三维SDF常用于计算机图形学、虚拟现实和机器人视觉等领域,因为它可以提供高效和准确的几何描述。通过使用三维SDF,我们可以执行空间中点的快速查询,以确定它们是否在模型内部或外部,以及它们到模型表面的最短距离。三维SDF是由二维SDF推广而来,其中二维SDF用于表示二维形状。
 shader
shader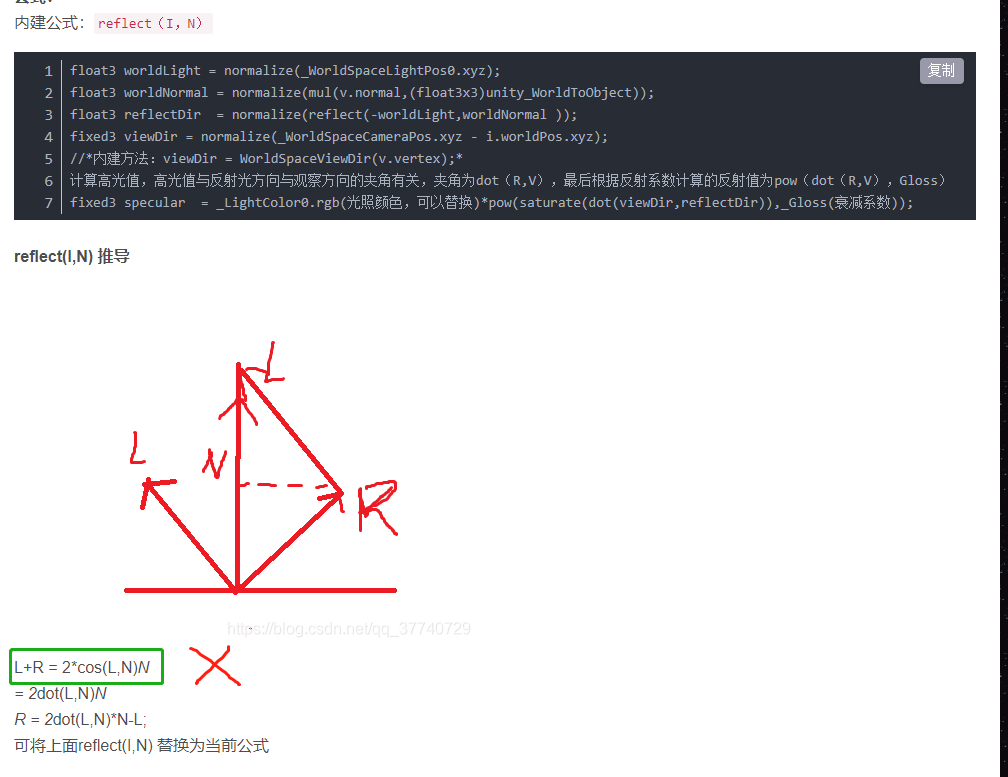

 threeJS
threeJS WebGL
WebGL
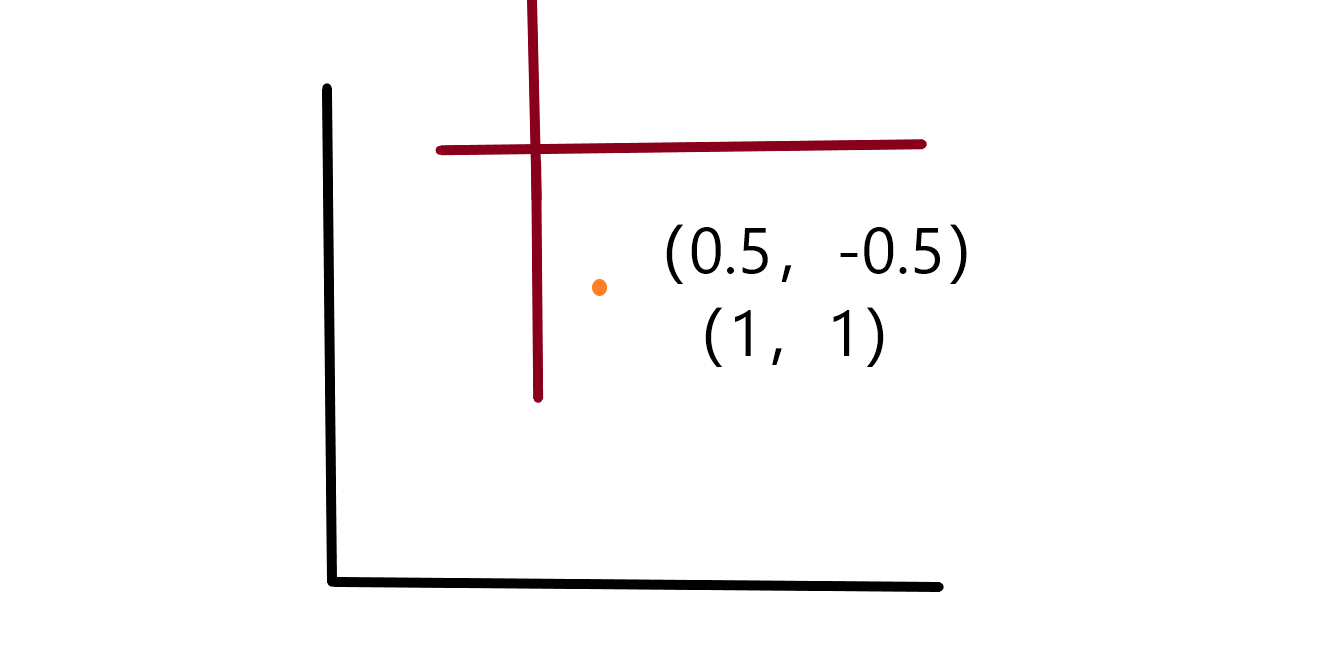









 cesium
cesium gis
gis 模型
模型 glsl
glsl webGPU
webGPU



